Python Challenges: Check a sequence of numbers is a geometric progression or not

Python Challenges - 1: Exercise-21 with Solution

Write a Python program to check a sequence of numbers is a geometric progression or not.

In mathematics, a geometric progression or geometric sequence is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
For example, the sequence 2, 6, 18, 54, ... is a geometric progression with common ratio 3. Similarly, 10, 5, 2.5, 1.25, ... is a geometric sequence with common ratio 1/2.

Explanation:

Sample Solution:-

Python Code:

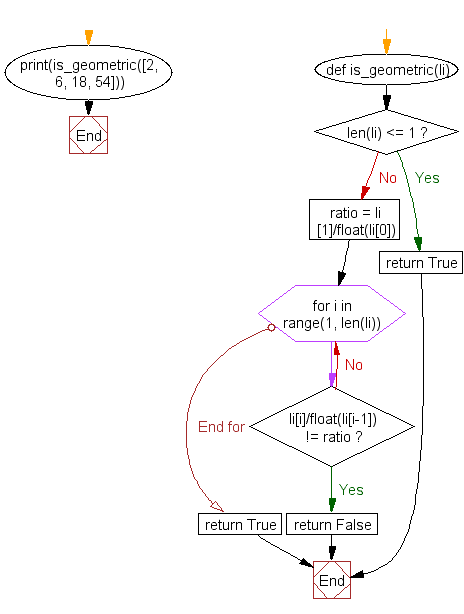
def is_geometric(li):
    if len(li) <= 1:
        return True
    # Calculate ratio
    ratio = li[1]/float(li[0])
    # Check the ratio of the remaining
    for i in range(1, len(li)):
        if li[i]/float(li[i-1]) != ratio: 
            return False
    return True 

print(is_geometric([2, 6, 18, 54]))

print(is_geometric([10, 5, 2.5, 1.25]))

print(is_geometric([5, 8, 9, 11]))

Sample Output:

True 
True
False

Flowchart:

Python Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Python program to check a sequence of numbers is an arithmetic progression or not.
Next: Write a Python program to compute the sum of the two reversed numbers and display the sum in reversed form.