Python Challenges: 3n + 1 Problem

Python Challenges - 1: Exercise-23 with Solution

Write a Python program where you take any positive integer n, if n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process until you reach 1.

According to Wikipedia, the Collatz conjecture is a conjecture in mathematics named after Lothar Collatz, who first proposed it in 1937. The conjecture is also known as the 3n + 1 conjecture.
The conjecture can be summarized as follows. Take any positive integer n. If n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process (which has been called "Half Or Triple Plus One") indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1.
Example:
For instance, starting with n = 12, one gets the sequence 12, 6, 3, 10, 5, 16, 8, 4, 2, 1.
n = 19, for example, takes longer to reach 1: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

Explanation:

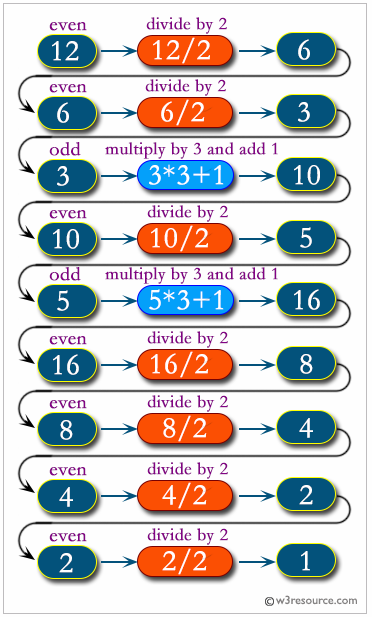
Sample Solution:

Python Code:

def collatz_sequence(x):
    num_seq = [x]
    if x < 1:
       return []
    while x > 1:
       if x % 2 == 0:
         x = x / 2
       else:
         x = 3 * x + 1
    # Added line
       num_seq.append(x)    
    return num_seq

print(collatz_sequence(12))

print(collatz_sequence(19))

Sample Output:

[12, 6.0, 3.0, 10.0, 5.0, 16.0, 8.0, 4.0, 2.0, 1.0]
[19, 58, 29.0, 88.0, 44.0, 22.0, 11.0, 34.0, 17.0, 52.0, 26.0, 13.0, 40.0, 20.0, 10.0, 5.0, 16.0, 8.0, 4.0, 2.
0, 1.0]

Flowchart:

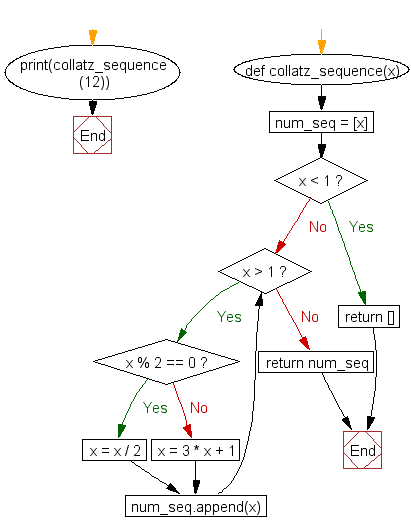
Python Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Python program to compute the sum of the two reversed numbers and display the sum in reversed form.
Next: Write a Python program to check whether a given number is an ugly number.