Java: Prove that Euclid’s algorithm computes the greatest common divisor of two positive given integers
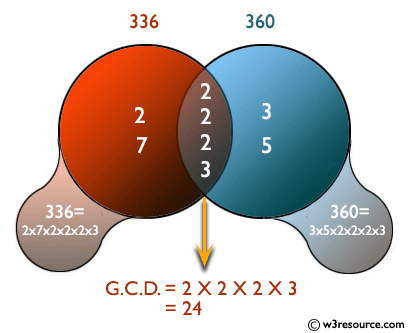
GCD Using Euclid's Algorithm
Write a Java program to prove that Euclid’s algorithm computes the greatest common divisor of two integers that have positive values.
According to Wikipedia "The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, they are the GCD of the original two numbers. By reversing the steps, the GCD can be expressed as a sum of the two original numbers each multiplied by a positive or negative integer, e.g., 21 = 5 × 105 + (−2) × 252. The fact that the GCD can always be expressed in this way is known as Bézout's identity."
Visual Presentation:
Sample Solution-1:
Java Code:
import java.util.Scanner;
public class Solution {
// Method to find the greatest common divisor using Euclidean algorithm
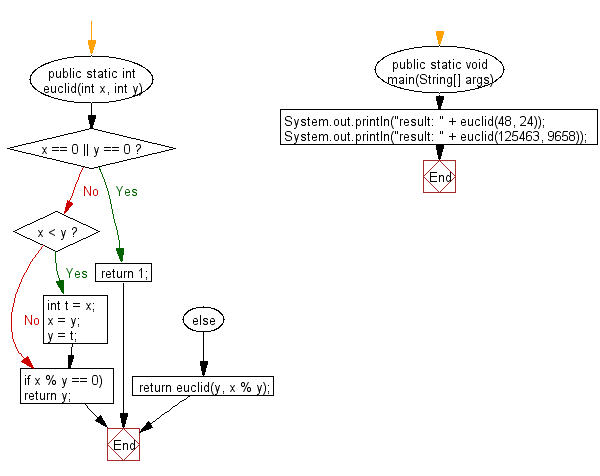
public static int euclid(int x, int y) {
// If either of the numbers is zero, return 1 as a special case
if (x == 0 || y == 0) {
return 1;
}
// If x is less than y, swap the values using a temporary variable
if (x < y) {
int t = x;
x = y;
y = t;
}
// Check if x is divisible by y
if (x % y == 0) {
return y; // Return y if it evenly divides x
} else {
return euclid(y, x % y); // Recursively call the euclid method with y and the remainder of x/y
}
}
public static void main(String[] args) {
// Displaying the result of the Euclidean algorithm for specific pairs of numbers
System.out.println("result: " + euclid(48, 24));
System.out.println("result: " + euclid(125463, 9658));
}
}
Sample Output:
result: 24 result: 1
Flowchart:
Sample Solution-2:
Java Code:
import java.util.Scanner;
public class Main {
// Method to find the greatest common divisor using Euclidean algorithm iteratively
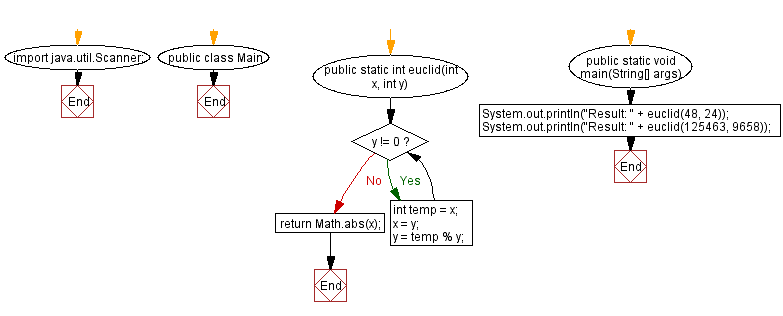
public static int euclid(int x, int y){
// Continue until y becomes zero
while (y != 0){
int temp = x; // Store the value of x in a temporary variable
x = y; // Assign y to x
y = temp % y; // Calculate the remainder of temp divided by y and assign it to y
}
return Math.abs(x); // Return the absolute value of x as the greatest common divisor
}
public static void main(String[] args) {
// Displaying the result of the Euclidean algorithm for specific pairs of numbers
System.out.println("Result: " + euclid(48, 24));
System.out.println("Result: " + euclid(125463, 9658));
}
}
Sample Output:
Result: 24 Result: 1
Flowchart:
For more Practice: Solve these Related Problems:
- Write a Java program to compute the GCD of two integers using a recursive implementation of Euclid's algorithm.
- Write a Java program to find the GCD of an array of integers by iteratively applying Euclid's algorithm.
- Write a Java program to calculate both the GCD and LCM of two numbers using Euclid's algorithm.
- Write a Java program to implement the extended Euclidean algorithm and output the Bézout coefficients.
Go to:
PREV : Largest Integer Base-2 Logarithm.
NEXT : 2D Prime Matrix.
Java Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
