Java: Divide a given array of integers into given k non-empty subsets whose sums are all equal

Last update on May 13 2025 13:00:18 (UTC/GMT +8 hours)

Divide Array into Equal Sum Subsets

Write a Java program to divide a given array of integers into given k non-empty subsets whose sums are all equal. Return true if all sums are equal otherwise return false.

Example:
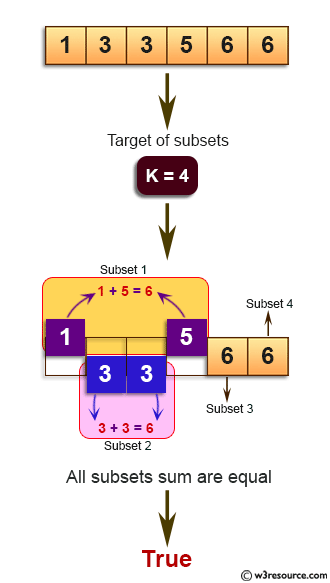
nums = {1,3,3,5,6,6}, k = 4;
4 subsets (5,1), (3, 3), (6), (6) with equal sums.

Visual Presentation:

Java Basic Exercises: Divide a given array of integers into given k non-empty subsets whose sums are all equal

Sample Solution:

Java Code:

// Import Arrays and other utility classes from java.util package
import java.util.Arrays;

// Main class for the solution
public class Solution {
    // Main method to execute the solution
    public static void main(String[] args) {
        // Sample input array and target value for testing subset partitioning
        int[] nums = {1, 3, 3, 5, 6, 6};
        int target = 4;

        // Display the original array
        System.out.print("Original Array: " + Arrays.toString(nums));

        // Display the target value for subsets
        System.out.print("\nTarget of subsets: " + target);

        // Display the result after removing duplicate characters using partition_k_subsets function
        System.out.print("\nAfter removing duplicate characters: " + partition_k_subsets(nums, target));
    }

    // Function to recursively search for valid subsets with a specific sum
    static boolean search_subset(int used, int n, boolean[] flag, int[] nums, int target) {
        // Base case: all elements used, subset found
        if (n == 0) {
            return true;
        }

        // Check if the current subset has not been considered before
        if (!flag[used]) {
            // Mark the current subset as visited
            flag[used] = true;

            // Calculate the remaining sum needed for the subset
            int remain_num = (n - 1) % target + 1;

            // Iterate through the elements in the array
            for (int i = 0; i < nums.length; i++) {
                // Check if the current element is not used in the subset and its value is less than or equal to the remaining sum
                if ((((used >> i) & 1) == 0) && nums[i] <= remain_num) {
                    // Recursively search for the subset with the updated parameters
                    if (search_subset(used | (1 << i), n - nums[i], flag, nums, target)) {
                        return true;
                    }
                }
            }
        }
        return false;
    }

    // Function to partition an array into k subsets with equal sum
    public static boolean partition_k_subsets(int[] nums, int k) {
        // Calculate the total sum of the elements in the array
        int sum = Arrays.stream(nums).sum();

        // Check if the sum is not divisible by k, return false
        if (sum % k > 0) {
            return false;
        }

        // Create a boolean array to track visited subsets
        boolean[] flag = new boolean[1 << nums.length];

        // Call the recursive search_subset function to check for valid subsets
        return search_subset(0, sum, flag, nums, sum / k);
    }
}

Sample Output:

Original Array: [1, 3, 3, 5, 6, 6]
Target of subsets: 4
After removing duplicate characters: true

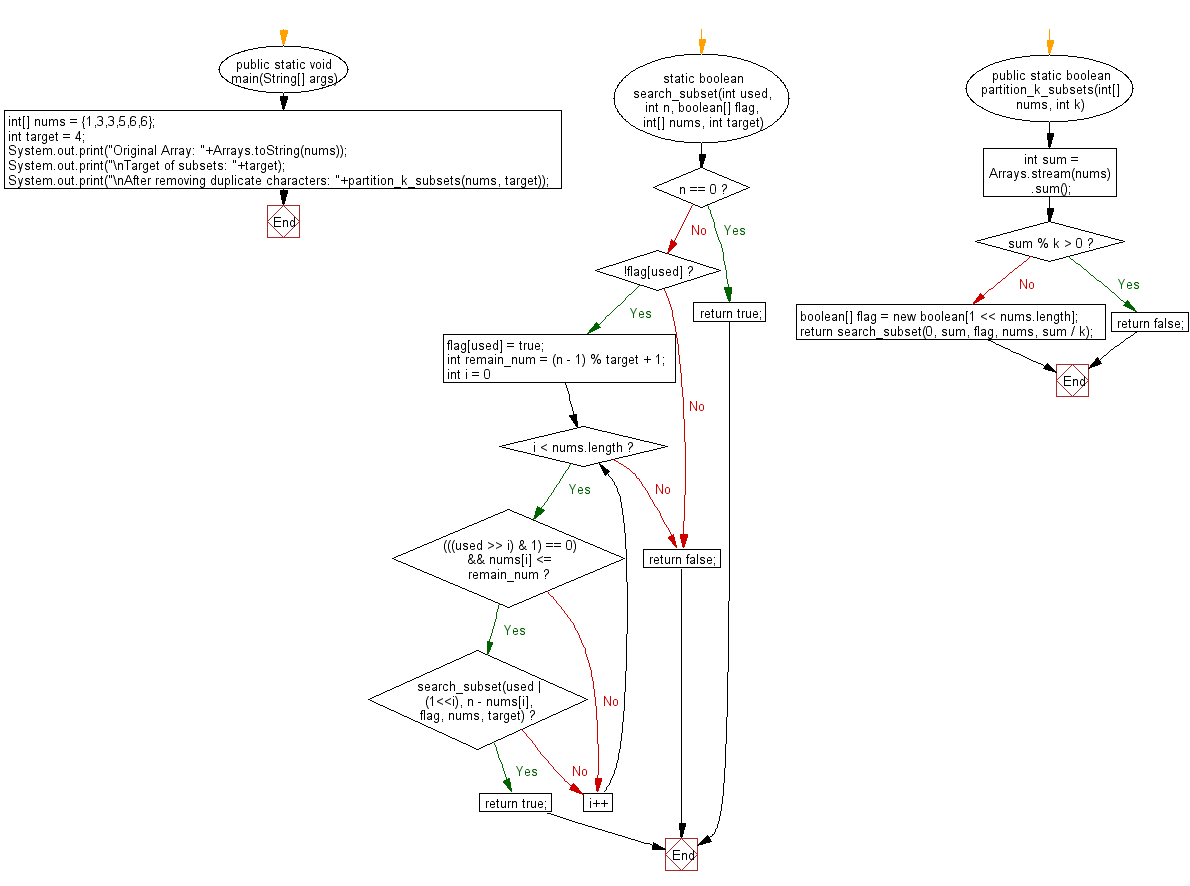
Flowchart:

Flowchart: Java exercises: Divide a given array of integers into given k non-empty subsets whose sums are all equal

For more Practice: Solve these Related Problems:

Write a Java program to partition an array into k subsets such that the difference between the subset sums is minimized.
Write a Java program to list all possible ways to divide an array into k non-empty subsets with equal sum using backtracking.
Write a Java program to determine the maximum k for which an array can be partitioned into subsets with equal sum.
Write a Java program to decide if an array can be partitioned into k equal sum subsets after removing exactly one element.

Go to:

PREV : Remove Duplicate Letters.
NEXT : Continuous Subarrays with Target Sum.

Java Code Editor:

Company: LinkedIn

Contribute your code and comments through Disqus.