JavaScript - Interpolation algorithm

JavaScript Searching Algorithm: Exercise-5 with Solution

Write a JavaScript program to find an element in a given sorted array of elements using Interpolation Search.

From Wikipedia:
Interpolation search is an algorithm for searching for a key in an array that has been ordered by numerical values assigned to the keys (key values). It was first described by W. W. Peterson in 1957. Interpolation search resembles the method by which people search a telephone directory for a name (the key value by which the book's entries are ordered): in each step the algorithm calculates where in the remaining search space the sought item might be, based on the key values at the bounds of the search space and the value of the sought key, usually via a linear interpolation. The key value actually found at this estimated position is then compared to the key value being sought. If it is not equal, then depending on the comparison, the remaining search space is reduced to the part before or after the estimated position. This method will only work if calculations on the size of differences between key values are sensible.

Test Data:
([1, 7, 13, 14, 15, 26, 37, 48, 99, 110], 13) -> 2
([1, 7, 13, 14, 15, 26, 37, 48, 99, 110], 26) -> 5
([1, 7, 13, 14, 15, 26, 37, 48, 99, 110], 0) -> -1
([1, 7, 13, 14, 15, 26, 37, 48, 99, 110], 99) ->8

Sample Solution:

JavaScript Code:

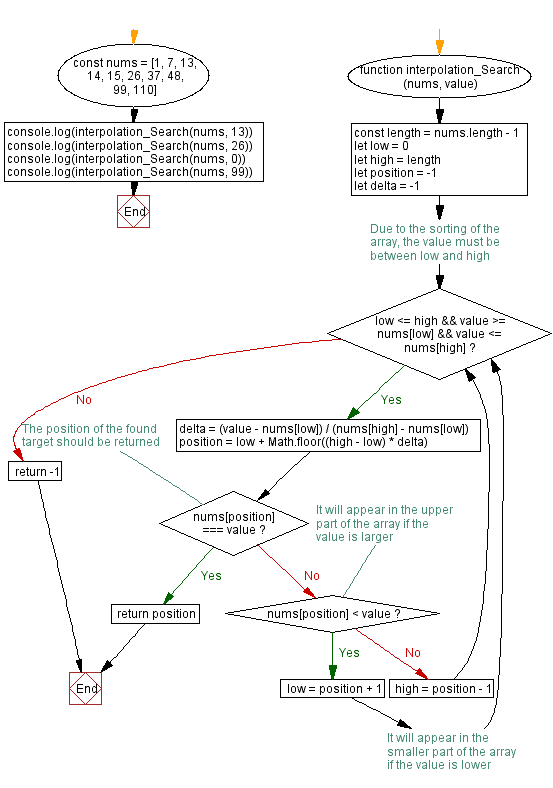
function interpolation_Search (nums, value) {
  const length = nums.length - 1
  let low = 0
  let high = length
  let position = -1
  let delta = -1
  // Due to the sorting of the array, the value must be between low and high
  while (low <= high && value >= nums[low] && value <= nums[high]) {
    delta = (value - nums[low]) / (nums[high] - nums[low])
    position = low + Math.floor((high - low) * delta)
    // The position of the found target should be returned
    if (nums[position] === value) {
      return position
    }
    // It will appear in the upper part of the array if the value is larger
    if (nums[position] < value) {
      low = position + 1
      // It will appear in the smaller part of the array if the value is lower
    } else {
      high = position - 1
    }
  }
  return -1
}
const nums = [1, 7, 13, 14, 15, 26, 37, 48, 99, 110]
console.log(interpolation_Search(nums, 13))
console.log(interpolation_Search(nums, 26))
console.log(interpolation_Search(nums, 0))
console.log(interpolation_Search(nums, 99))

Sample Output:

2
5
-1
8

Flowchart:

Live Demo:

See the Pen javascript-searching-algorithm-exercise-5 by w3resource (@w3resource) on CodePen.

* To run the code mouse over on Result panel and click on 'RERUN' button.*

Improve this sample solution and post your code through Disqus

Previous: Jump search algorithm.