Python List Advanced Exercise - Implement a LRU cache

Python List Advanced: Exercise-13 with Solution

From Wikipedia -
Least recently used (LRU)
Discards the least recently used items first. This algorithm requires keeping track of what was used when, which is expensive if one wants to make sure the algorithm always discards the least recently used item. General implementations of this technique require keeping "age bits" for cache-lines and track the "Least Recently Used" cache-line based on age-bits. In such an implementation, every time a cache-line is used, the age of all other cache-lines changes. LRU is actually a family of caching algorithms with members including 2Q by Theodore Johnson and Dennis Shasha, and LRU/K by Pat O'Neil, Betty O'Neil and Gerhard Weikum.

Write a Python a function to implement a LRU cache.

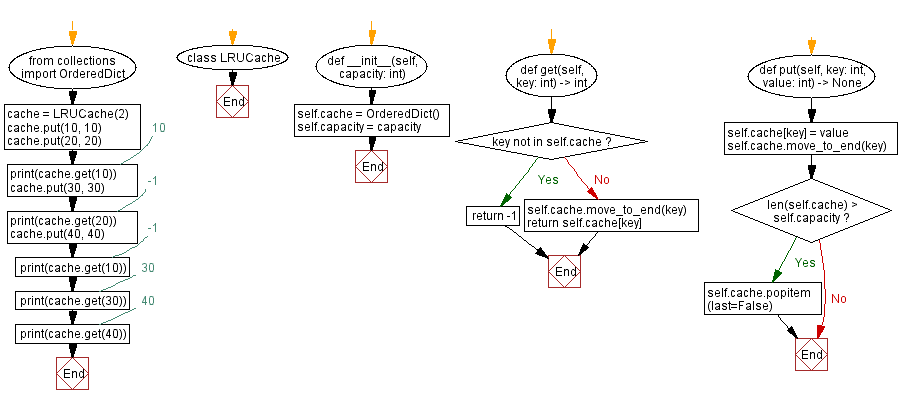
In the following function, the OrderedDict, specialized container datatypes from collections module is used to store the key-value pairs in the cache, with the ordering reflecting the least recently used item. If the key exists, the get method returns it; otherwise, it returns -1. When the put method is used, the value for the given key is added or updated, and the key-value pair is moved to the end of the order to reflect that it was recently used. When the cache size exceeds the capacity, the least recently used item is removed by popping the first item from the OrderedDict.

Sample Solution:

Python Code:

# Import the 'OrderedDict' class from the 'collections' module
from collections import OrderedDict

# Define a class 'LRUCache' for a Least Recently Used (LRU) cache
class LRUCache:
    # Initialize the LRUCache with a specified capacity
    def __init__(self, capacity: int):
        # Create an ordered dictionary 'cache' to store key-value pairs
        self.cache = OrderedDict()
        # Set the capacity of the cache
        self.capacity = capacity

    # Get the value associated with a key from the cache
    def get(self, key: int) -> int:
        # Check if the key is not in the cache
        if key not in self.cache:
            return -1
        else:
            # Move the accessed key to the end to mark it as most recently used
            self.cache.move_to_end(key)
            # Return the value associated with the key
            return self.cache[key]

    # Put a key-value pair into the cache
    def put(self, key: int, value: int) -> None:
        # Update the cache with the key-value pair
        self.cache[key] = value
        # Move the key to the end to mark it as most recently used
        self.cache.move_to_end(key)
        # Check if the cache size exceeds the specified capacity
        if len(self.cache) > self.capacity:
            # Remove the least recently used item (the first item) from the cache
            self.cache.popitem(last=False)

# Create an instance of the LRUCache class with a capacity of 2
cache = LRUCache(2)

# Put key-value pairs into the cache
cache.put(10, 10)
cache.put(20, 20)

# Get the value associated with key 10 from the cache
print(cache.get(10))   # 10

# Put another key-value pair into the cache, which causes the eviction of the least recently used item (key 20)
cache.put(30, 30)

# Get the value associated with key 20, which is not in the cache
print(cache.get(20))   # -1 

# Put another key-value pair into the cache, which causes the eviction of the least recently used item (key 10)
cache.put(40, 40)

# Get the value associated with key 10, which is not in the cache
print(cache.get(10))   # -1 

# Get the values associated with keys 30, and 40 from the cache
print(cache.get(30))   # 30
print(cache.get(40))   # 40 

Sample Output:

10
-1
-1
30
40

Flowchart:

What is the time complexity and space complexity of the following Python code?

from collections import OrderedDict
class LRUCache:
    def __init__(self, capacity: int):
        self.cache = OrderedDict()
        self.capacity = capacity

    def get(self, key: int) -> int:
        if key not in self.cache:
            return -1
        else:
            self.cache.move_to_end(key)
            return self.cache[key]

    def put(self, key: int, value: int) -> None:
        self.cache[key] = value
        self.cache.move_to_end(key)
        if len(self.cache) > self.capacity:
            self.cache.popitem(last=False)

Time complexity - The time complexity of get and put methods in the LRUCache class are both O(1). Caches are implemented using OrderedDicts from the collections module, which provide constant time complexity for insertion, deletion, and lookup.

Space complexity - The space complexity of the LRUCache class is O(capacity), where capacity is the maximum number of key-value pairs that can be stored in the cache. This is because the size of the cache is directly proportional to the capacity parameter passed to the constructor.

Python Code Editor:

Previous: First non-repeated element in a list.
Next: Sort a list of dictionaries based on values of a key.