Python: Test AB and CD are orthogonal or not

Last update on April 17 2025 13:01:26 (UTC/GMT +8 hours)

Orthogonal Line Checker

There are four different points on a plane, P(x_p,y_p), Q(x_q, y_q), R(x_r, y_r) and S(x_s, y_s). Write a Python program to determine whether AB and CD are orthogonal.

Input:
x_p,y_p, x_q, y_q, x_r, y_r, x_s and y_s are -100 to 100 respectively and each value can be up to 5 digits after the decimal point It is given as a real number including the number of.
Output:
Output AB and CD are not orthogonal! or AB and CD are orthogonal!.

Sample Solution:

Python Code:

# Infinite loop to continuously prompt the user for input
while True:
    try:
        # Print statement to prompt the user to input coordinates of points xp, yp, xq, yq, xr, yr, xs, ys
        print("Input xp, yp, xq, yq, xr, yr, xs, ys:")
        
        # Take user input for the coordinates of points and convert them to float
        x_p, y_p, x_q, y_q, x_r, y_r, x_s, y_s = map(float, input().split())
        
        # Calculate vectors pq and rs
        pq_x, pq_y = x_q - x_p, y_q - y_p
        rs_x, rs_y = x_s - x_r, y_s - y_r
        
        # Calculate the dot product of pq and rs
        rs = pq_x * rs_x + pq_y * rs_y
        
        # Check if the dot product is close to zero, and print the result accordingly
        if abs(rs) > 1e-10:
            print("AB and CD are not orthogonal!")
        else:
            print("AB and CD are orthogonal!")
    
    # Exception handling to break out of the loop if an error occurs (e.g., invalid input)
    except:
        break

Sample Output:

Input xp, yp, xq, yq, xr, yr, xs, ys:
 4.5 -2.5 -2.5 4.5 3.5 3.5 3.8 -3.5
AB and CD are not orthogonal!

Explanation:

Here is a breakdown of the above Python code:

The code enters an infinite loop using "while True".
Inside the loop, it prompts the user to input coordinates of points xp, yp, xq, yq, xr, yr, xs, ys.
It takes user input for the coordinates and converts them to float.
It calculates vectors pq and rs using the input coordinates.
It calculates the dot product of 'pq' and 'rs'.
It checks if the dot product is close to zero (within a tolerance), and prints the result accordingly.
Exception handling is used to break out of the loop if an error occurs, such as invalid input.

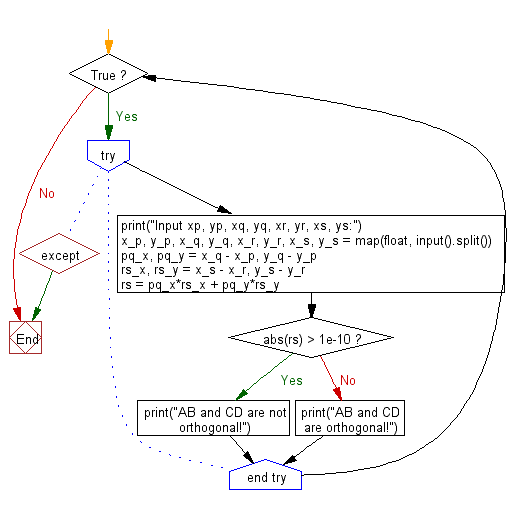
Flowchart:

For more Practice: Solve these Related Problems:

Write a Python program to check if two line segments are perpendicular given their endpoints using vector dot product.
Write a Python program to determine orthogonality of lines by comparing the slopes derived from two pairs of points.
Write a Python program to calculate the angle between two lines and verify if it equals 90 degrees.
Write a Python program to check if two lines are orthogonal by ensuring their slopes are negative reciprocals.

Go to:

Previous: Write a Python program to create maximum number of regions obtained by drawing n given straight lines.
Next: Write a Python program to sum of all numerical values (positive integers) embedded in a sentence.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.