Python List Advanced Exercise - Longest common sub-sequence in two lists

Python List Advanced: Exercise-11 with Solution

Write a Python function to find the longest common sub-sequence in two lists.

Sample Solution:

Python Code:

# Define a function to find the longest common subsequence between two lists
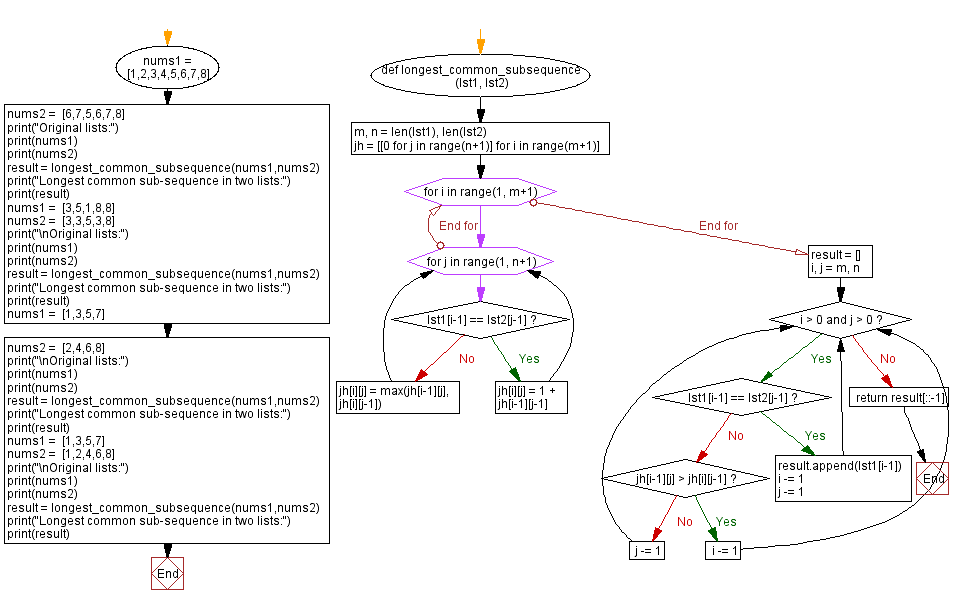
def longest_common_subsequence(lst1, lst2):
    # Get the lengths of both input lists
    m, n = len(lst1), len(lst2)
    # Initialize a 2D table 'jh' to store the lengths of common subsequences
    jh = [[0 for j in range(n+1)] for i in range(m+1)]

    # Fill in the 'jh' table using dynamic programming
    for i in range(1, m+1):
        for j in range(1, n+1):
            if lst1[i-1] == lst2[j-1]:
                jh[i][j] = 1 + jh[i-1][j-1]
            else:
                jh[i][j] = max(jh[i-1][j], jh[i][j-1])

    # Initialize a result list to store the common subsequence
    result = []
    i, j = m, n

    # Reconstruct the longest common subsequence
    while i > 0 and j > 0:
        if lst1[i-1] == lst2[j-1]:
            result.append(lst1[i-1])
            i -= 1
            j -= 1
        elif jh[i-1][j] > jh[i][j-1]:
            i -= 1
        else:
            j -= 1

    # Return the result list in reverse order to get the correct sequence
    return result[::-1]

# Create two lists of numbers
nums1 =  [1, 2, 3, 4, 5, 6, 7, 8]
nums2 =  [6, 7, 5, 6, 7, 8]

# Print the original lists of numbers
print("Original lists:")
print(nums1)
print(nums2)

# Call the longest_common_subsequence function with the two number lists and store the result in 'result'
result = longest_common_subsequence(nums1, nums2)

# Print the result, which is the longest common subsequence between the two lists
print("Longest common sub-sequence in two lists:")
print(result)

# Create two more lists of numbers
nums1 =  [3, 5, 1, 8, 8]
nums2 =  [3, 3, 5, 3, 8]

# Print the original lists of numbers
print("\nOriginal lists:")
print(nums1)
print(nums2)

# Call the longest_common_subsequence function with the second pair of number lists and store the result in 'result'
result = longest_common_subsequence(nums1, nums2)

# Print the result, which is the longest common subsequence between the two lists
print("Longest common sub-sequence in two lists:")
print(result)

# Create two lists of numbers that have no common elements
nums1 =  [1, 3, 5, 7]
nums2 =  [2, 4, 6, 8]

# Print the original lists of numbers
print("\nOriginal lists:")
print(nums1)
print(nums2)

# Call the longest_common_subsequence function with the third pair of number lists and store the result in 'result'
result = longest_common_subsequence(nums1, nums2)

# Print the result, which is an empty list since there is no common subsequence
print("Longest common sub-sequence in two lists:")
print(result)

# Create two lists of numbers with some common elements
nums1 =  [1, 3, 5, 7]
nums2 =  [1, 2, 4, 6, 8]

# Print the original lists of numbers
print("\nOriginal lists:")
print(nums1)
print(nums2)

# Call the longest_common_subsequence function with the fourth pair of number lists and store the result in 'result'
result = longest_common_subsequence(nums1, nums2)

# Print the result, which is the longest common subsequence between the two lists
print("Longest common sub-sequence in two lists:")
print(result) 

Sample Output:

Original lists:
[1, 2, 3, 4, 5, 6, 7, 8]
[6, 7, 5, 6, 7, 8]
Longest common sub-sequence in two lists:
[5, 6, 7, 8]

Original lists:
[3, 5, 1, 8, 8]
[3, 3, 5, 3, 8]
Longest common sub-sequence in two lists:
[3, 5, 8]

Original lists:
[1, 3, 5, 7]
[2, 4, 6, 8]
Longest common sub-sequence in two lists:
[]

Original lists:
[1, 3, 5, 7]
[1, 2, 4, 6, 8]
Longest common sub-sequence in two lists:
[1]

Flowchart:

What is the time complexity and space complexity of the following Python code?

def longest_common_subsequence(lst1, lst2):
    m, n = len(lst1), len(lst2)
    jh = [[0 for j in range(n+1)] for i in range(m+1)]
    
    for i in range(1, m+1):
        for j in range(1, n+1):
            if lst1[i-1] == lst2[j-1]:
                jh[i][j] = 1 + jh[i-1][j-1]
            else:
                jh[i][j] = max(jh[i-1][j], jh[i][j-1])
    
    result = []
    i, j = m, n
    while i > 0 and j > 0:
        if lst1[i-1] == lst2[j-1]:
            result.append(lst1[i-1])
            i -= 1
            j -= 1
        elif jh[i-1][j] > jh[i][j-1]:
            i -= 1
        else:
            j -= 1
    
    return result[::-1]

Time complexity - The time complexity of the said code is O(mn), where m and n are the lengths of the input lists “lst1” and “lst2”, respectively. The code uses dynamic programming to compute the length of the longest common subsequence of “lst1” and “lst2”, which requires filling in a table with dimensions (m+1) x (n+1). The loop that fills in this table has O(mn) iterations, and each iteration takes constant time, so the overall time complexity is O(mn). The loop that constructs the result list by backtracking through the table also takes O(m+n) time, but this is dominated by the O(mn) time complexity of the dynamic programming loop.

Space complexity - The space complexity of the said code is O(mn), where m and n are the lengths of the input lists “lst1” and “lst2”, respectively. This is because the code creates a two-dimensional list jh with dimensions (m+1) x (n+1) to store the dynamic programming table. Each element of “jh” is a single integer, so the total space used by “jh” is proportional to its dimensions, which are O(mn). The result list also has space complexity proportional to the length of the longest common subsequence, which is at most min(m, n), so we can consider it to be O(min(m, n)) space complexity. However, since this is a constant factor that does not depend on the size of the input lists, we can ignore it and say that the overall space complexity is O(mn).

Python Code Editor:

Previous: Minimum sum sub-sequence in a list.
Next: First non-repeated element in a list.