Python List Advanced Exercise - Minimum sum sub-sequence in a list

Python List Advanced: Exercise-10 with Solution

Write a Python a function to find the minimum sum sub-sequence in a list. Return the sub-sequence.

Sample Solution:

Python Code:

# Define a function to find the minimum sum subsequence in a list
def minimum_sum_subsequence(lst):
    # Initialize the minimum sum as positive infinity
    min_sum = float('inf')
    # Initialize variables to track the start and end indices of the minimum sum subsequence
    start, end = 0, 0
    # Initialize variables to track the current start index and current sum
    curr_start, curr_sum = 0, 0

    # Iterate through the elements of the list
    for i in range(len(lst)):
        # Add the current element to the current sum
        curr_sum += lst[i]
        # Check if the current sum is less than the minimum sum
        if curr_sum < min_sum:
            # Update the minimum sum and the corresponding start and end indices
            min_sum = curr_sum
            start = curr_start
            end = i
        # If the current sum becomes positive, reset it to 0 and update the current start index
        if curr_sum > 0:
            curr_sum = 0
            curr_start = i + 1

    # Return the subsequence from the start index to the end index
    return lst[start:end + 1]

# Create a list of numbers
nums =  [1, 2, 6, 12]

# Print the original list of numbers
print("Original list:")
print(nums)

# Call the minimum_sum_subsequence function with the list and store the result in 'result'
result = minimum_sum_subsequence(nums)

# Print the result, which is the minimum sum subsequence of the list
print("Minimum sum sub-sequence of the said list:")
print(result)

# Create another list of numbers, including negative values
nums =  [1, -2, 4, 3, 5, 4, 6, 9, 2, -10]

# Print the original list of numbers
print("\nOriginal list:")
print(nums)

# Call the minimum_sum_subsequence function with the second list and store the result in 'result'
result = minimum_sum_subsequence(nums)

# Print the result, which is the minimum sum subsequence of the list
print("Minimum sum sub-sequence of the said list:")
print(result)

# Create another list of numbers, including negative values and positive values
nums =  [2, 4, -3, -5, -4, 6, 9, 2]

# Print the original list of numbers
print("\nOriginal list:")
print(nums)

# Call the minimum_sum_subsequence function with the third list and store the result in 'result'
result = minimum_sum_subsequence(nums)

# Print the result, which is the minimum sum subsequence of the list
print("Minimum sum sub-sequence of the said list:")
print(result)

# Create another list of numbers, including negative values and a negative sum subsequence
nums =  [1, 2, 4, 3, 5, -24, 4, 9, -22]

# Print the original list of numbers
print("\nOriginal list:")
print(nums)

# Call the minimum_sum_subsequence function with the fourth list and store the result in 'result'
result = minimum_sum_subsequence(nums)

# Print the result, which is the minimum sum subsequence of the list
print("Minimum sum sub-sequence of the said list:")
print(result) 

Sample Output:

Original list:
[1, 2, 6, 12]
Minimum sum sub-sequence of the said list:
[1]

Original list:
[1, -2, 4, 3, 5, 4, 6, 9, 2, -10]
Minimum sum sub-sequence of the said list:
[-10]

Original list:
[2, 4, -3, -5, -4, 6, 9, 2]
Minimum sum sub-sequence of the said list:
[-3, -5, -4]

Original list:
[1, 2, 4, 3, 5, -24, 4, 9, -22]
Minimum sum sub-sequence of the said list:
[-24, 4, 9, -22]

Flowchart:

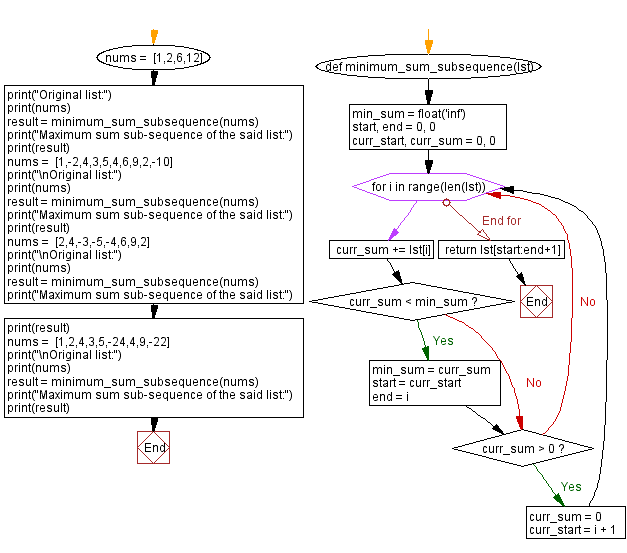
What is the time complexity and space complexity of the following Python code?

def minimum_sum_subsequence(lst):
    min_sum = float('inf')
    start, end = 0, 0
    curr_start, curr_sum = 0, 0
    
    for i in range(len(lst)):
        curr_sum += lst[i]
        if curr_sum < min_sum:
            min_sum = curr_sum
            start = curr_start
            end = i
        if curr_sum > 0:
            curr_sum = 0
            curr_start = i + 1
    
    return lst[start:end+1]

Time complexity - The time complexity of the said code is O(n), where n is the length of the input list “lst”. This is because the code iterates through the input list once to find the minimum sum subsequence. The loop (for loop) has O(n) iterations, and each iteration takes constant time, so the overall time complexity is O(n).

Space complexity - The space complexity of the said code is also O(1). This is because the code only uses a fixed amount of memory that does not depend on the size of the input list. Specifically, it uses a constant amount of memory to store the variables "min_sum", "start", "end", "curr_start", and "curr_sum", regardless of the length of the input list "lst".
The output list also has space complexity proportional to the length of the minimum sum subsequence, but since this is a constant factor that does not depend on the size of the input list "lst", we can consider it to be O(1) space complexity as well.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Maximum sum sub-sequence in a list.
Next: Longest common sub-sequence in two lists.