Python List Advanced Exercise - Maximum sum sub-sequence in a list
9. Maximum Sum Sub-sequence
Write a Python a function to find the maximum sum sub-sequence in a list. Return the maximum value.
Sample Solution:
Python Code:
# Define a function to find the maximum sum subsequence in an array
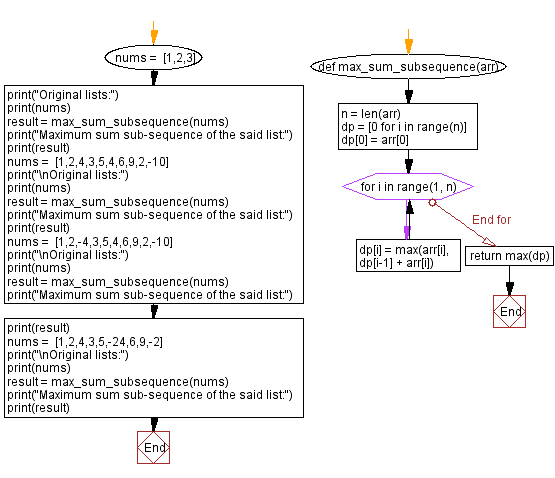
def max_sum_subsequence(arr):
n = len(arr)
# Initialize a dynamic programming (DP) array 'dp' with all zeros
dp = [0 for i in range(n)]
# Set the first element of 'dp' to the first element of 'arr'
dp[0] = arr[0]
# Iterate through the array from the second element
for i in range(1, n):
# Calculate the maximum sum at the current position by comparing the element itself and the sum from the previous position
dp[i] = max(arr[i], dp[i-1] + arr[i])
# Return the maximum value in the 'dp' array, which represents the maximum sum subsequence
return max(dp)
# Create a list of numbers
nums = [1, 2, 3]
# Print the original list of numbers
print("Original list:")
print(nums)
# Call the max_sum_subsequence function with the list and store the result in 'result'
result = max_sum_subsequence(nums)
# Print the result, which is the maximum sum subsequence of the list
print("Maximum sum sub-sequence of the said list:")
print(result)
# Create another list of numbers
nums = [1, 2, 4, 3, 5, 4, 6, 9, 2, -10]
# Print the original list of numbers
print("\nOriginal list:")
print(nums)
# Call the max_sum_subsequence function with the second list and store the result in 'result'
result = max_sum_subsequence(nums)
# Print the result, which is the maximum sum subsequence of the list
print("Maximum sum sub-sequence of the said list:")
print(result)
# Create another list of numbers with negative values
nums = [1, 2, -4, 3, 5, 4, 6, 9, 2, -10]
# Print the original list of numbers
print("\nOriginal list:")
print(nums)
# Call the max_sum_subsequence function with the third list and store the result in 'result'
result = max_sum_subsequence(nums)
# Print the result, which is the maximum sum subsequence of the list
print("Maximum sum sub-sequence of the said list:")
print(result)
# Create another list of numbers with a negative value in the middle
nums = [1, 2, 4, 3, 5, -24, 6, 9, -2]
# Print the original list of numbers
print("\nOriginal list:")
print(nums)
# Call the max_sum_subsequence function with the fourth list and store the result in 'result'
result = max_sum_subsequence(nums)
# Print the result, which is the maximum sum subsequence of the list
print("Maximum sum sub-sequence of the said list:")
print(result)
Sample Output:
Original lists: [1, 2, 3] Maximum sum sub-sequence of the said list: 6 Original lists: [1, 2, 4, 3, 5, 4, 6, 9, 2, -10] Maximum sum sub-sequence of the said list: 36 Original lists: [1, 2, -4, 3, 5, 4, 6, 9, 2, -10] Maximum sum sub-sequence of the said list: 29 Original lists: [1, 2, 4, 3, 5, -24, 6, 9, -2] Maximum sum sub-sequence of the said list: 15
Flowchart:
What is the time complexity and space complexity of the following Python code?
def max_sum_subsequence(arr):
n = len(arr)
dp = [0 for i in range(n)]
dp[0] = arr[0]
for i in range(1, n):
dp[i] = max(arr[i], dp[i-1] + arr[i])
return max(dp)
Time complexity - The time complexity of the said code is O(n), where n is the length of the input array "arr". The code iterates through the input array to fill the dp array, which takes O(n) time, and then finds the maximum value in the "dp" array, which also takes O(n) time. Therefore, the overall time complexity is O(n).
Space complexity - The space complexity of the said code is also O(n). This is because the code creates a new array "dp" of length n, which takes O(n) space. Therefore, the overall space complexity is O(n).
For more Practice: Solve these Related Problems:
- Write a Python function to find the maximum sum subarray using Kadane's algorithm.
- Write a Python function to compute the maximum contiguous sub-sequence sum with dynamic programming.
- Write a Python function to return both the maximum sum and the corresponding sub-sequence from a list of numbers.
- Write a Python function to implement a recursive approach to find the maximum sum subarray and compare it with the iterative method.
Go to:
Previous: Preserve order by removing duplicates.
Next: Minimum sum sub-sequence in a list.
Python Code Editor:
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
