Python Math: Implement Euclidean Algorithm to compute the greatest common divisor

Last update on April 24 2025 12:34:52 (UTC/GMT +8 hours)

76. Euclidean Algorithm for GCD

Write a Python program to implement the Euclidean Algorithm to compute the greatest common divisor (GCD).

Note: In mathematics, the Euclidean algorithm[a], or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two numbers, the largest number that divides both of them without leaving a remainder.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 147 = 252 − 105.

Sample Solution:

Python Code:

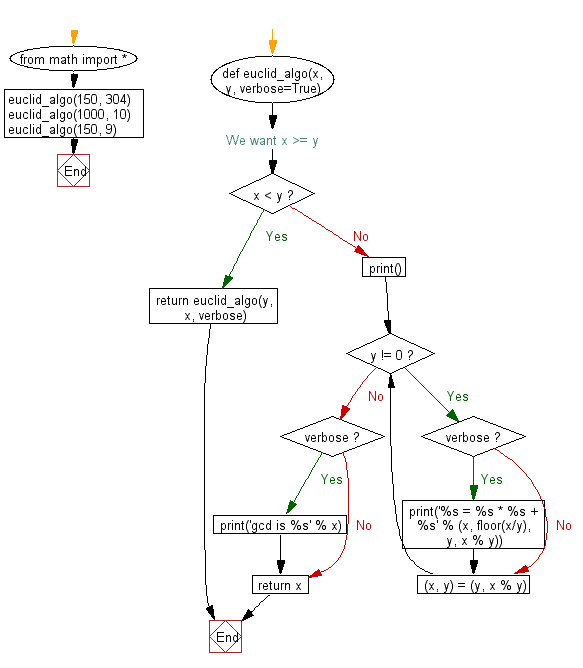
from math import *

def euclid_algo(x, y, verbose=True):
	if x < y: # We want x >= y
		return euclid_algo(y, x, verbose)
	print()
	while y != 0:
		if verbose: print('%s = %s * %s + %s' % (x, floor(x/y), y, x % y))
		(x, y) = (y, x % y)
	
	if verbose: print('gcd is %s' % x) 
	return x


euclid_algo(150, 304)
euclid_algo(1000, 10)
euclid_algo(150, 9)

Sample Output:

304 = 2 * 150 + 4                                                                                             
150 = 37 * 4 + 2                                                                                              
4 = 2 * 2 + 0                                                                                                 
gcd is 2                                                                                                      
                                                                                                              
1000 = 100 * 10 + 0                                                                                           
gcd is 10                                                                                                     
                                                                                                              
150 = 16 * 9 + 6                                                                                              
9 = 1 * 6 + 3                                                                                                 
6 = 2 * 3 + 0                                                                                                 
gcd is 3

Pictorial Presentation:

Flowchart:

For more Practice: Solve these Related Problems:

• Write a Python program that implements the Euclidean algorithm to compute the GCD of two numbers and prints each step of the division process.
• Write a Python function that takes two integers, applies the Euclidean algorithm recursively to find the GCD, and returns both the GCD and the sequence of remainders.
• Write a Python script to compute the GCD of multiple pairs of numbers using the Euclidean algorithm and then compare the results with math.gcd().
• Write a Python program to prompt the user for two integers, calculate their GCD using the Euclidean method, and then print the step-by-step process.

Go to:

• Python Math Exercises Home ↩
• Python Exercises Home ↩

Previous: Write a Python program to calculate clusters using Hierarchical Clustering method.
Next: Write a Python program to convert RGB color to HSV color.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.