Understanding language with the Transformer model

Last update on November 14 2023 07:14:54 (UTC/GMT +8 hours)

A new architecture called Transformers has recently emerged that has been shown to outperform the RNN-based seq2seq models in several NLP tasks. It is capable of modeling global dependencies between input and output sequences. It was introduced in 2017 by Ashish Vaswani, et. al., in the NeurIPS paper Attention Is All You Need. The Transformer architecture is based on a concept called attention, and more specifically, the self-attention mechanism. Having the attention mechanism would mean that our model would be able to learn to focus on the parts of an input sequence that are more relevant to the sentiment.

This article is an excerpt from the book Python Machine Learning, Third Edition by Sebastian Raschka and Vahid Mirjalili. This book is a comprehensive guide to machine learning and deep learning with Python. This new third edition is updated for TensorFlow 2 and the latest additions to scikit-learn. In this article, we are going to covered the Transformer model.

Understanding the self-attention mechanism

This section will explain the self-attention mechanism and how it helps a Transformer model to focus on important parts of a sequence for NLP. The first subsection will cover a very basic form of self-attention to illustrate the overall idea behind learning text representations. Then, we will add different weight parameters so that we arrive at the self-attention mechanism as commonly used in the Transformer model.

A basic version of self-attention

To introduce the basic idea behind self-attention, let's assume we have an input sequence of length T, x⁽⁰⁾,x⁽¹⁾,…,x^(T), as well as an output sequence, y⁽⁰⁾,y⁽¹⁾,…,y^(T). Each element of these sequences, x^(t) and y^(t), are vectors of size d (i.e., x^(t)∈R^d). For a seq2seq task, the goal of self-attention is to model the dependencies of each element in the output sequence to the input elements. In order to achieve this, attention mechanisms are composed of three stages. Firstly, we derive importance weights based on the similarity between the current element and all other elements in the sequence. Secondly, we normalize the weights, which usually involves the use of the already familiar softmax function. Thirdly, we use these weights in combination with the corresponding sequence elements in order to compute the attention value.

More formally, the output of self-attention is the weighted sum of all input sequences. For instance, for the ith input element, the corresponding output value is computed as follows:

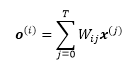
Here, the weights, W_ij, are computed based on the similarity between the current input element, x⁽ⁱ⁾, and all other elements in the input sequence. More concretely, this similarity is computed as the dot product between the current input element, x⁽ⁱ⁾, and another element in the input sequence, x^(j):

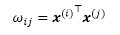
After computing these similarity-based weights for the ith input and all inputs in the sequence (x⁽ⁱ⁾ to x^(T)), the "raw" weights (ω_i0 to ω_iT) are then normalized using the familiar softmax function, as follows:

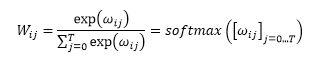
Notice that as a consequence of applying the softmax function, the weights will sum to 1 after this normalization, i.e.,

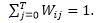
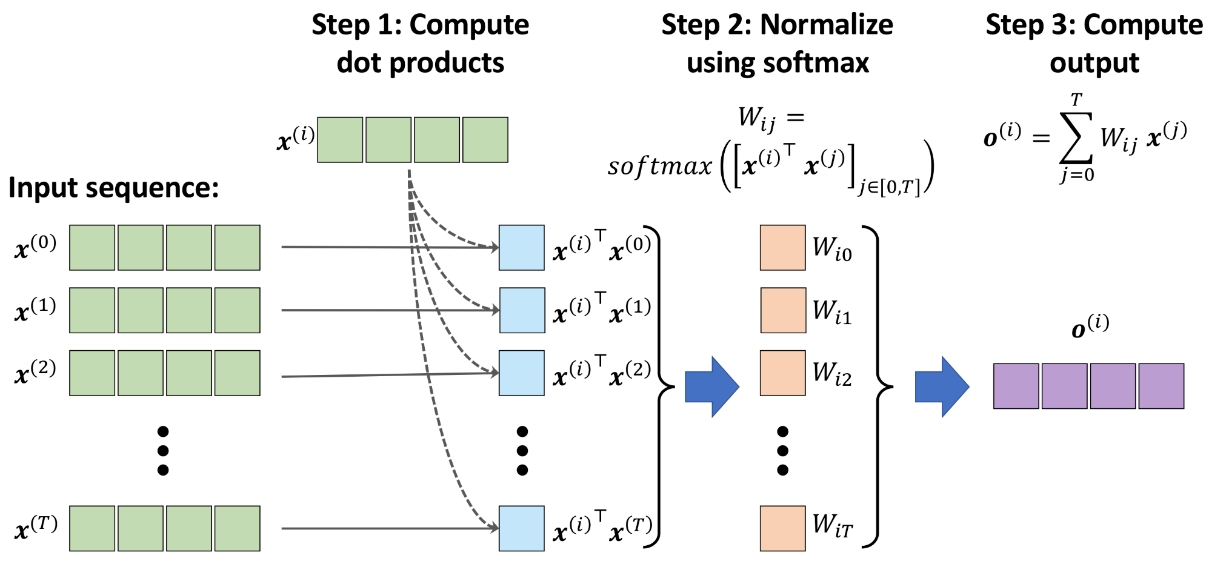
To recap, let's summarize the three main steps behind the self-attention operation:

For a given input element, x⁽ⁱ⁾, and each jth element in the range [0,T], compute the dot product,
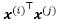
Obtain the weight, W_ij, by normalizing the dot products using the softmax function
Compute the output, o⁽ⁱ⁾, as the weighted sum over the entire input sequence:

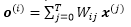
These steps are further illustrated in the following figure:

Parameterizing the self-attention mechanism with query, key, and value weights

Now that you have been introduced to the basic concept behind self-attention, this subsection summarizes the more advanced self-attention mechanism that is used in the Transformer model. Note that in the previous subsection, we didn't involve any learnable parameters when computing the outputs. Hence, if we want to learn a language model and want to change the attention values to optimize an objective, such as minimizing the classification error, we will need to change the word embeddings (i.e., input vectors) that underlie each input element, x⁽ⁱ⁾. In other words, using the previously introduced basic self-attention mechanism, the Transformer model is rather limited with regard to how it can update or change the attention values during model optimization for a given sequence. To make the self-attention mechanism more flexible and amenable to model optimization, we will introduce three additional weight matrices that can be fit as model parameters during model training. We denote these three weight matrices as U_q, U_k, and U_v. They are used to project the inputs into query, key, and value sequence elements:

Query sequence: q⁽ⁱ⁾=U_q x⁽ⁱ⁾ for i∈[0,T],
Key sequence: k⁽ⁱ⁾=U_k x⁽ⁱ⁾ for i∈[0,T],
Value sequence: v⁽ⁱ⁾=U_v x⁽ⁱ⁾ for i∈[0,T]

Here, both q⁽ⁱ and k⁽ⁱ⁾ are vectors of size d_k. Therefore, the projection matrices U_q and U_k have the shape d_k×d, while U_v has the shape d_v×d. For simplicity, we can design these vectors to have the same shape, for example, using m=d_k=d_v. Now, instead of computing the unnormalized weight as the pairwise dot product between the given input sequence element, x⁽ⁱ⁾, and the jth sequence element, x^(j), we can compute the dot product between the query and key:

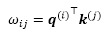
We can then further use m, or, more precisely, 1/√m, to scale ω_ij before normalizing it via the softmax function, as follows:

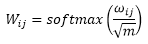
Note that scaling ω¬_ij by 1/√m will ensure that the Euclidean length of the weight vectors will be approximately in the same range.

Multi-head attention and the Transformer block

Another trick that greatly improves the discriminatory power of the self-attention mechanism is multi-head attention (MHA), which combines multiple self-attention operations together. In this case, each self-attention mechanism is called a head, which can be computed in parallel. Using r parallel heads, each head results in a vector, h, of size m. These vectors are then concatenated to obtain a vector, z, with the shape r ×m. Finally, the concatenated vector is projected using the output matrix W^o to obtain the final output, as follows:

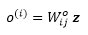
The architecture of a Transformer block is shown in the following figure:

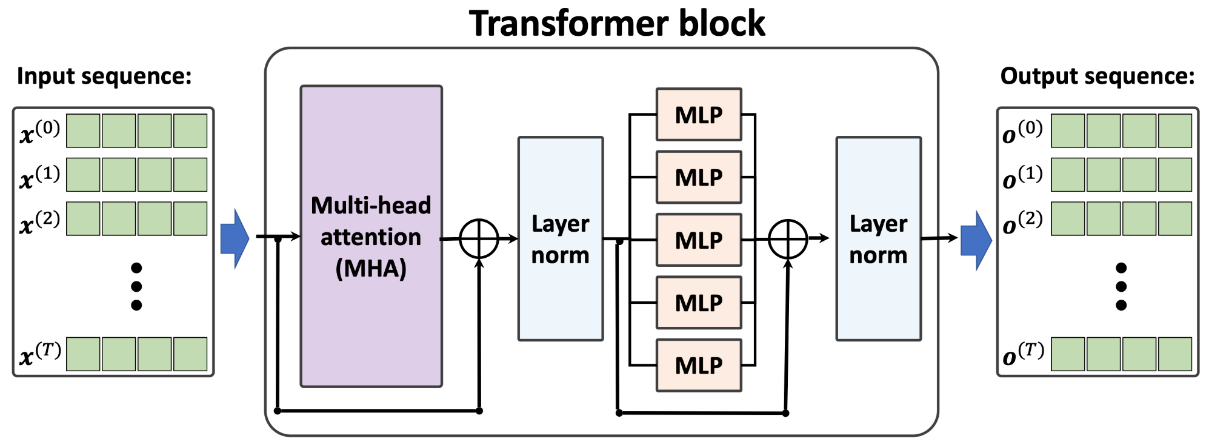
Notice that in the Transformer architecture shown in the previous figure, we added two additional components that we haven't discussed yet. One of these components is the residual connection, which adds the output from a layer (or even a group of layers) to its input, i.e., x+layer(x). The block consisting of a layer (or multiple layers) with such a residual connection is called a residual block. The Transformer block shown in the previous figure has two residual blocks.

The other new component is layer normalization, which is denoted in the previous figure as "Layer norm." There is a family of normalization layers including batch normalization, which we will cover in. For now, you can think of layer normalization as a fancy or more advanced way to normalize or scale the NN inputs and activations in each layer.

Returning to the illustration of the Transformer model in the previous figure, let's now discuss how this model works. First, the input sequence is passed to the MHA layers, which is based on the self-attention mechanism that we discussed earlier. In addition, the input sequences are added to the output of the MHA layers via the residual connections—this ensures that the earlier layers will receive sufficient gradient signals during training, which is a common trick that is used to improve training speed and convergence. If you are interested, you can read more about the concept behind residual connections in the research article Deep Residual Learning for Image Recognition by Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun.

After the input sequences are added to the output of the MHA layers, the outputs are normalized via layer normalization. These normalized signals then go through a series of MLP (i.e., fully connected) layers, which also have a residual connection. Finally, the output from the residual block is normalized again and returned as the output sequence, which can be used for sequence classification or sequence generation.

In this article, we covered the Transformer model, which leverages the self-attention mechanism in order to focus on the relevant parts of a sequence. Python Machine Learning, Third Edition is a comprehensive guide to machine learning and deep learning with Python.

About the Authors

Sebastian Raschka is an Assistant Professor of Statistics at the University of Wisconsin-Madison focusing on machine learning and deep learning research. Some of his recent research methods have been applied to solving problems in the field of biometrics for imparting privacy to face images. Other research focus areas include the development of methods related to model evaluation in machine learning, deep learning for ordinal targets, and applications of machine learning to computational biology.

Vahid Mirjalili obtained his Ph.D. in mechanical engineering working on novel methods for large-scale, computational simulations of molecular structures. Currently, he is focusing his research efforts on applications of machine learning in various computer vision projects at the Department of Computer Science and Engineering at Michigan State University. He recently joined 3M Company as a research scientist, where he uses his expertise and applies state-of-the-art machine learning and deep learning techniques to solve real-world problems in various applications to make life better.