C Exercises: Check whether a triangle is Equilateral, Isosceles or Scalene

C Conditional Statement: Exercise-14 with Solution

Write a C program to check whether a triangle is Equilateral, Isosceles or Scalene.

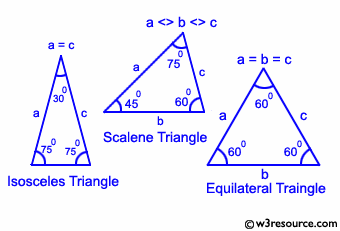
Equilateral triangle: An equilateral triangle is a triangle in which all three sides are equal. In the familiar Euclidean geometry, equilateral triangles are also equiangular; that is, all three internal angles are also congruent to each other and are each 60°.

Isosceles triangle: An isosceles triangle is a triangle that has two sides of equal length.

Scalene triangle: A scalene triangle is a triangle that has three unequal sides, such as those illustrated above.

Visual Presentation:

Sample Solution:

C Code:

#include <stdio.h>  // Include the standard input/output header file.

int main()
{
    int sidea, sideb, sidec; // Declare variables for the sides of the triangle.
    /*
     * Reads all sides of a triangle
     */
    printf("Input three sides of triangle: ");  // Prompt user for input.
    scanf("%d %d %d", &sidea, &sideb, &sidec);  // Read and store the sides of the triangle.
    // Check if the sides form a valid triangle
    if ((sidea + sideb > sidec) && (sidea + sidec > sideb) && (sideb + sidec > sidea)) {
        // If the sides form a valid triangle, continue with the classification
        if(sidea==sideb && sideb==sidec) // Check if all sides are equal.
        {
            printf("This is an equilateral triangle.\n");  // Print message for equilateral triangle.
        }
        else if(sidea==sideb || sidea==sidec || sideb==sidec) // Check if two sides are equal.
        {
            printf("This is an isosceles triangle.\n");  // Print message for isosceles triangle.
        }
        else // If no sides are equal.
        {
            printf("This is a scalene triangle.\n");  // Print message for scalene triangle.
        }
    } else {
        // If the sides do not form a valid triangle
        printf("Input sides do not form a valid triangle.\n");
    }
    return 0;
} 

Sample Output:

Input three sides of triangle: 50 50 60                                                                       
This is an isosceles triangle.

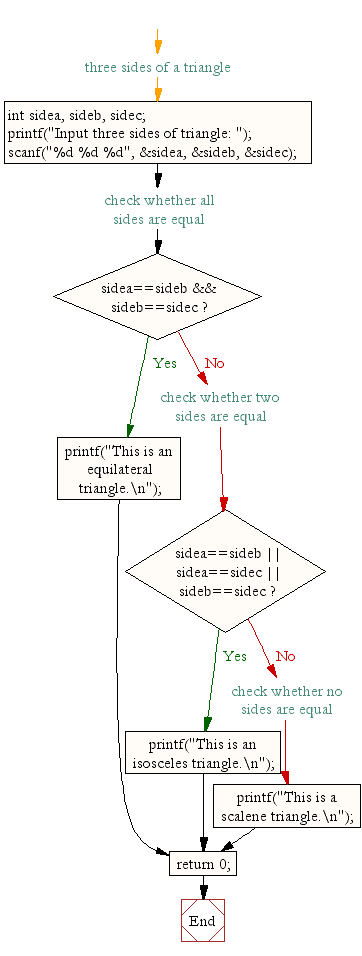
Flowchart:

C Programming Code Editor:

Previous: Write a C program to read temperature in centigrade and display a suitable message according to temperature state below.
Next: Write a C program to check whether a triangle can be formed by the given value for the angles.