C Exercises: Check Armstrong and perfect numbers
9. Armstrong & Perfect Number Function Variants
Write a program in C to check Armstrong and Perfect numbers using the function.
Pictorial Presentation:
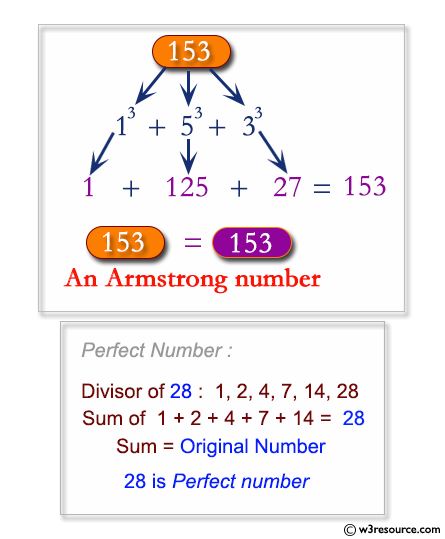
Sample Solution:
C Code:
#include <stdio.h>
int checkArmstrong(int n1);
int checkPerfect(int n1);
int main()
{
int n1;
printf("\n\n Function : check Armstrong and perfect numbers :\n");
printf("-----------------------------------------------------\n");
printf(" Input any number: ");
scanf("%d", &n1);
//Calls the isArmstrong() function
if(checkArmstrong(n1))
{
printf(" The %d is an Armstrong number.\n", n1);
}
else
{
printf(" The %d is not an Armstrong number.\n", n1);
}
//Calls the checkPerfect() function
if(checkPerfect(n1))
{
printf(" The %d is a Perfect number.\n\n", n1);
}
else
{
printf(" The %d is not a Perfect number.\n\n", n1);
}
return 0;
}
// Checks whether a three digits number is Armstrong number or not.
//An Armstrong number is an n-digit number that is equal
//to the sum of the n-th powers of its digits.
int checkArmstrong(int n1)
{
int ld, sum, num;
sum = 0;
num = n1;
while(num!=0)
{
ld = num % 10; // find the last digit of the number
sum += ld * ld * ld; //calculate the cube of the last digit and adds to sum
num = num/10;
}
return (n1 == sum);
}
// Checks whether the number is perfect number or not.
//a perfect number is a positive integer that is equal to
//the sum of its positive divisors excluding the number itself
int checkPerfect(int n1)
{
int i, sum, num;
sum = 0;
num = n1;
for(i=1; i<num; i++)
{
/* If i is a divisor of n1 */
if(num%i == 0)
{
sum += i;
}
}
return (n1 == sum);
}
Sample Output:
Function : check armstrong and perfect numbers : ----------------------------------------------------- Input any number: 371 The 371 is an Armstrong number. The 371 is not a Perfect number.
Explanation:
int checkArmstrong(int n1) {
int ld, sum, num;
sum = 0;
num = n1;
while (num != 0) {
ld = num % 10; // find the last digit of the number
sum += ld * ld * ld; //calculate the cube of the last digit and adds to sum
num = num / 10;
}
return (n1 == sum);
}
The function 'checkArmstrong' takes a single argument 'n1' of type int. It checks whether the input number 'n1' is an Armstrong number or not. An Armstrong number is a number that is equal to the sum of the cubes of its digits.
The function initializes three local integer variables, 'ld', 'sum', and 'num', to 0, 0, and the value of n1 respectively. It then enters a while loop that continues as long as num is not equal to 0. In each iteration of the loop, the function computes the last digit of num by taking the modulus of num with 10 and storing it in ld. It then adds the cube of 'ld' to 'sum'. Finally, it updates the value of num by dividing it by 10. This loop computes the sum of the cubes of the digits of 'n1' and stores it in 'sum'. The function then returns a boolean value that indicates whether 'n1' is equal to sum or not.
Time complexity and space complexity:
The time complexity of this function is O(log n), where n is the input number n1, because the while loop iterates log_10(n) times to compute the sum of the cubes of the digits of n1.
The space complexity of this function is O(1), as it only uses a fixed amount of memory to store the three integer variables ld, sum, and num.
int checkPerfect(int n1) {
int i, sum, num;
sum = 0;
num = n1;
for (i = 1; i < num; i++) {
/* If i is a divisor of n1 */
if (num % i == 0) {
sum += i;
}
}
return (n1 == sum);
}
The function 'checkPerfect' takes a single argument 'n1' of type int. It checks whether the input number 'n1' is a perfect number or not. A perfect number is a number that is equal to the sum of its proper divisors. The function initializes three local integer variables, 'i', 'sum', and 'num', to 1, 0, and the value of 'n1' respectively. It then enters a for loop that iterates from 1 to num-1. In each iteration of the loop, the function checks whether 'i' is a divisor of num by computing num % i. If 'i' is a divisor of ‘num’, it adds 'i' to 'sum'. Finally, the loop completes and the function returns a boolean value that indicates whether n1 is equal to sum or not.
Time complexity and space complexity:
The time complexity of this function is O(n), where n is the input number n1, because the for loop iterates n-1 times to compute the sum of the proper divisors of n1.
The space complexity of this function is O(1), as it only uses a fixed amount of memory to store the three integer variables 'i', 'sum', and 'num'.
Flowchart:
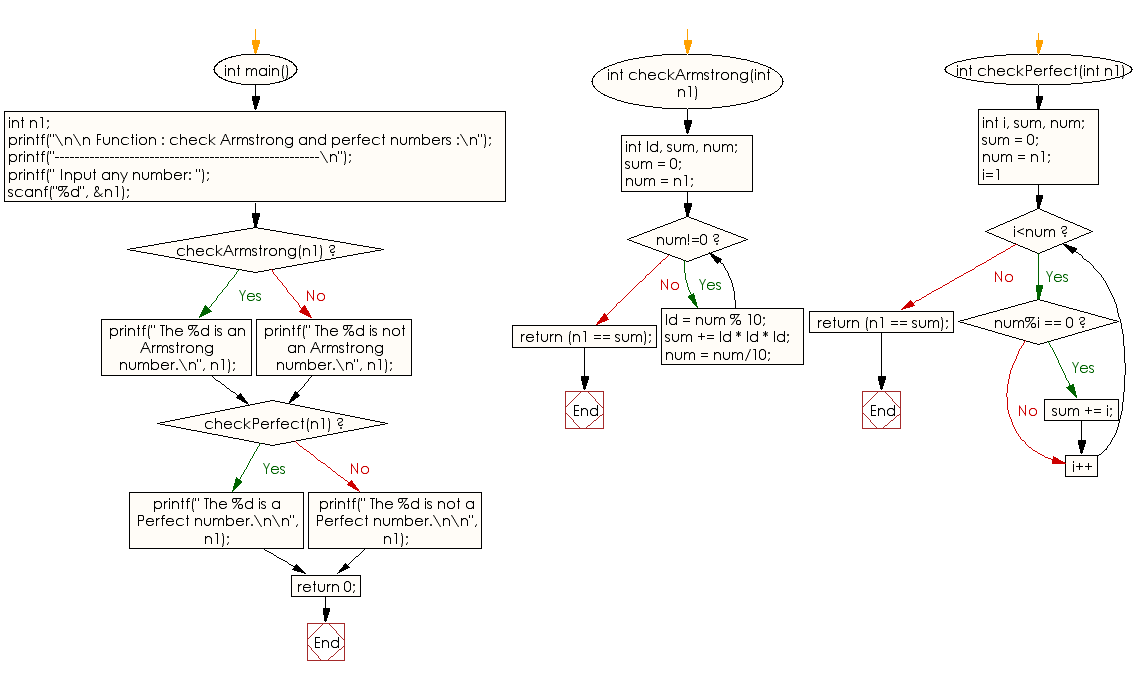
For more Practice: Solve these Related Problems:
- Write a C program to check if a number is an Armstrong number using a function that sums powered digits.
- Write a C program to verify if a number is perfect by calculating the sum of its proper divisors within a function.
- Write a C program to list Armstrong numbers within a given range by repeatedly invoking a checking function.
- Write a C program to display both Armstrong and Perfect numbers from a specified range using separate functions.
Go to:
PREV : Largest Element in Array Function Variants.
NEXT :
Perfect Numbers in Range Function Variants.
C Programming Code Editor:
Improve this sample solution and post your code through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
