Topological sorting of directed Acyclic Graph (DAG) in C

C Program to implement Graph Structure: Exercise-7 with Solution

Write a C program to perform topological sorting on a directed acyclic graph (DAG).

From Wikipedia,

In computer science, a topological sort or topological ordering of a directed graph is a linear ordering of its vertices such that for every directed edge (u,v) from vertex u to vertex v, u comes before v in the ordering. For instance, the vertices of the graph may represent tasks to be performed, and the edges may represent constraints that one task must be performed before another; in this application, a topological ordering is just a valid sequence for the tasks. Precisely, a topological sort is a graph traversal in which each node v is visited only after all its dependencies are visited. A topological ordering is possible if and only if the graph has no directed cycles, that is, if it is a directed acyclic graph (DAG). Any DAG has at least one topological ordering, and algorithms are known for constructing a topological ordering of any DAG in linear time. Topological sorting has many applications, especially in ranking problems such as feedback arc set. Topological sorting is possible even when the DAG has disconnected components.

Example ( Topological sorting ):

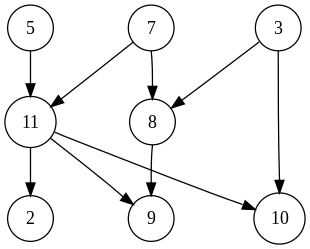
This graph has many valid topological sorts, including:

• 5, 7, 3, 11, 8, 2, 9, 10 (visual left-to-right, top-to-bottom)
• 3, 5, 7, 8, 11, 2, 9, 10 (smallest-numbered available vertex first)
• 3, 5, 7, 8, 11, 2, 10, 9 (lexicographic by incoming neighbors)
• 5, 7, 3, 8, 11, 2, 10, 9 (fewest edges first)
• 7, 5, 11, 3, 10, 8, 9, 2 (largest-numbered available vertex first)
• 5, 7, 11, 2, 3, 8, 9, 10 (attempting top-to-bottom, left-to-right)
• 3, 7, 8, 5, 11, 10, 2, 9 (arbitrary)

Source: Wikipdeia

Sample Solution:

C Code:

#include <stdio.h>
#include <stdlib.h>
	
#define MAX_VERTICES 100

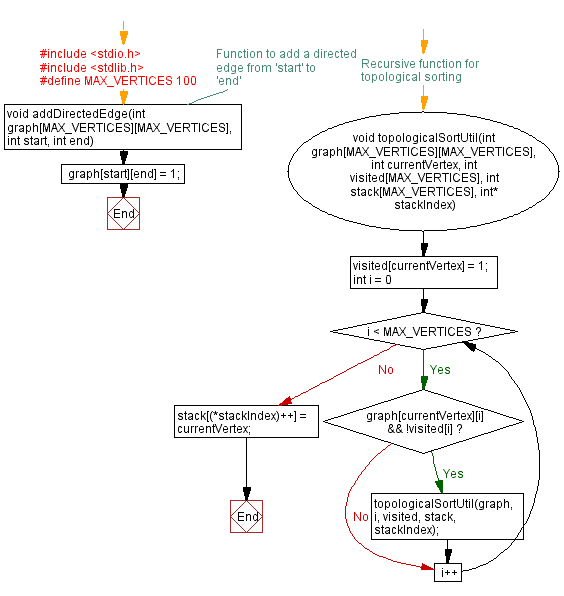
// Function to add a directed edge from 'start' to 'end'
void addDirectedEdge(int graph[MAX_VERTICES][MAX_VERTICES], int start, int end) {
    graph[start][end] = 1;
}

// Recursive function for topological sorting
void topologicalSortUtil(int graph[MAX_VERTICES][MAX_VERTICES], int currentVertex, int visited[MAX_VERTICES], int stack[MAX_VERTICES], int* stackIndex) {
    visited[currentVertex] = 1;

    for (int i = 0; i < MAX_VERTICES; i++) {
        if (graph[currentVertex][i] && !visited[i]) {
            topologicalSortUtil(graph, i, visited, stack, stackIndex);
        }
    }

    stack[(*stackIndex)++] = currentVertex;
}

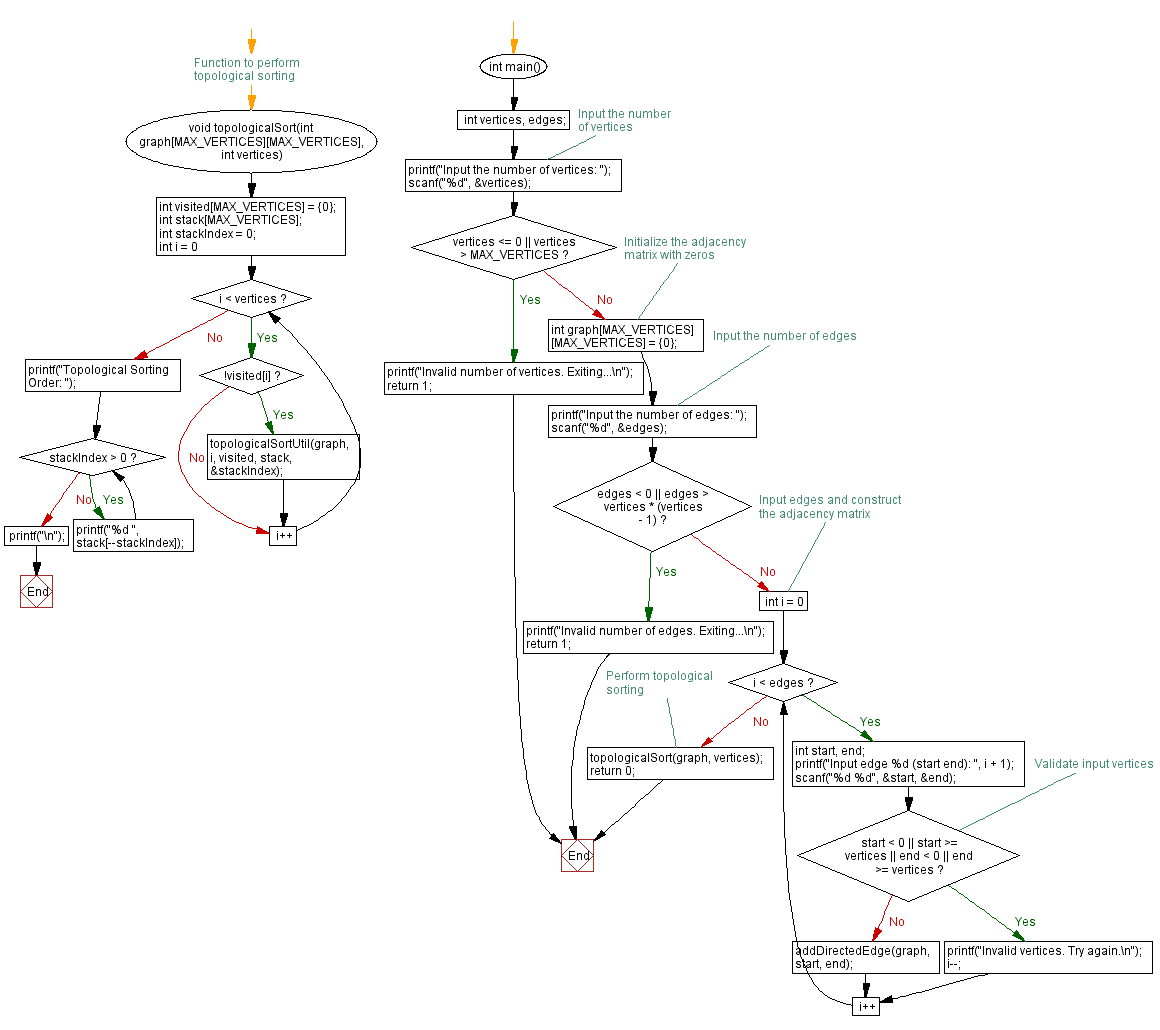
// Function to perform topological sorting
void topologicalSort(int graph[MAX_VERTICES][MAX_VERTICES], int vertices) {
    int visited[MAX_VERTICES] = {0};
    int stack[MAX_VERTICES];
    int stackIndex = 0;

    for (int i = 0; i < vertices; i++) {
        if (!visited[i]) {
            topologicalSortUtil(graph, i, visited, stack, &stackIndex);
        }
    }

    printf("Topological Sorting Order: ");
    while (stackIndex > 0) {
        printf("%d ", stack[--stackIndex]);
    }
    printf("\n");
}

int main() {
    int vertices, edges;

    // Input the number of vertices
    printf("Input the number of vertices: ");
    scanf("%d", &vertices);

    if (vertices <= 0 || vertices > MAX_VERTICES) {
        printf("Invalid number of vertices. Exiting...\n");
        return 1;
    }

    int graph[MAX_VERTICES][MAX_VERTICES] = {0}; // Initialize the adjacency matrix with zeros

    // Input the number of edges
    printf("Input the number of edges: ");
    scanf("%d", &edges);

    if (edges < 0 || edges > vertices * (vertices - 1)) {
        printf("Invalid number of edges. Exiting...\n");
        return 1;
    }

    // Input edges and construct the adjacency matrix
    for (int i = 0; i < edges; i++) {
        int start, end;
        printf("Input edge %d (start end): ", i + 1);
        scanf("%d %d", &start, &end);

        // Validate input vertices
        if (start < 0 || start >= vertices || end < 0 || end >= vertices) {
            printf("Invalid vertices. Try again.\n");
            i--;
            continue;
        }

        addDirectedEdge(graph, start, end);
    }

    // Perform topological sorting
    topologicalSort(graph, vertices);

    return 0;
}

Output:

Input the number of vertices: 6
Input the number of edges: 7
Input edge 1 (start end): 5 2
Input edge 2 (start end): 5 0
Input edge 3 (start end): 4 0
Input edge 4 (start end): 4 1
Input edge 5 (start end): 2 3
Input edge 6 (start end): 3 1
Input edge 7 (start end): 1 3
Topological Sorting Order: 5 4 2 1 3 0

Explanation:

In the exercise above,

• addDirectedEdge Function
• This function adds a directed edge from the 'start' vertex to the 'end' vertex in the adjacency matrix.
• topologicalSortUtil Function:
• This is a recursive function used for DFS traversal and topological sorting.
• It marks the current vertex as visited and recursively calls itself for adjacent vertices.
• The vertices are pushed onto a stack during recursive calls.
• topologicalSort Function:
• This function initializes an array to keep track of visited vertices and a stack for storing the topological order.
• It calls the "topologicalSortUtil()" function for each unvisited vertex.
• After completing the DFS traversal, it prints the topological sorting order by popping elements from the stack.
• main Function:
• It takes input for the number of vertices and edges.
• It reads the edges and constructs the adjacency matrix.
• Calls the "topologicalSort()" function to print the topological order.

Flowchart:

C Programming Code Editor:

Previous: Cycle detection in Graph: C Program implementation.
Next: Prim's Algorithm for minimum Spanning Tree in C.