C Exercises: Binary searching

Last update on March 20 2025 12:37:43 (UTC/GMT +8 hours)

21. Binary Search Recursion Variants

Write a program in C for binary search using recursion.

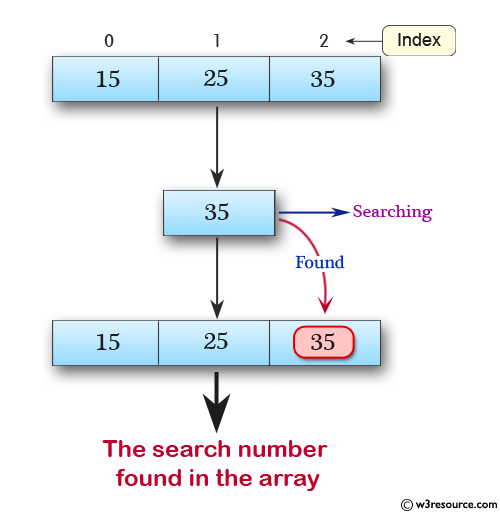
Pictorial Presentation:

Sample Solution:

C Code:

#include <stdio.h>
int binarySearch(int*, int, int, int, int);

int main()
{
    int arr1[10], i, n, md, c, low, hg;

    printf("\n\n Recursion : Binary searching :\n");
    printf("-----------------------------------\n");
    printf(" Input the number of elements to store in the array :");
    scanf("%d", &n);
    printf(" Input %d numbers of elements in the array in ascending order :\n", n);
    for (i = 0; i < n; i++) 
    {
        printf(" element - %d : ", i);
        scanf("%d", &arr1[i]);
    }
    printf(" Input the number to search : ");
    scanf("%d", &md);
    low = 0, hg = n - 1;
    c = binarySearch(arr1, n, md, low, hg);
    if (c == 0)
        printf(" The search number not exists in the array.\n\n");
    else
        printf(" The search number found in the array.\n\n");
    return 0;
}

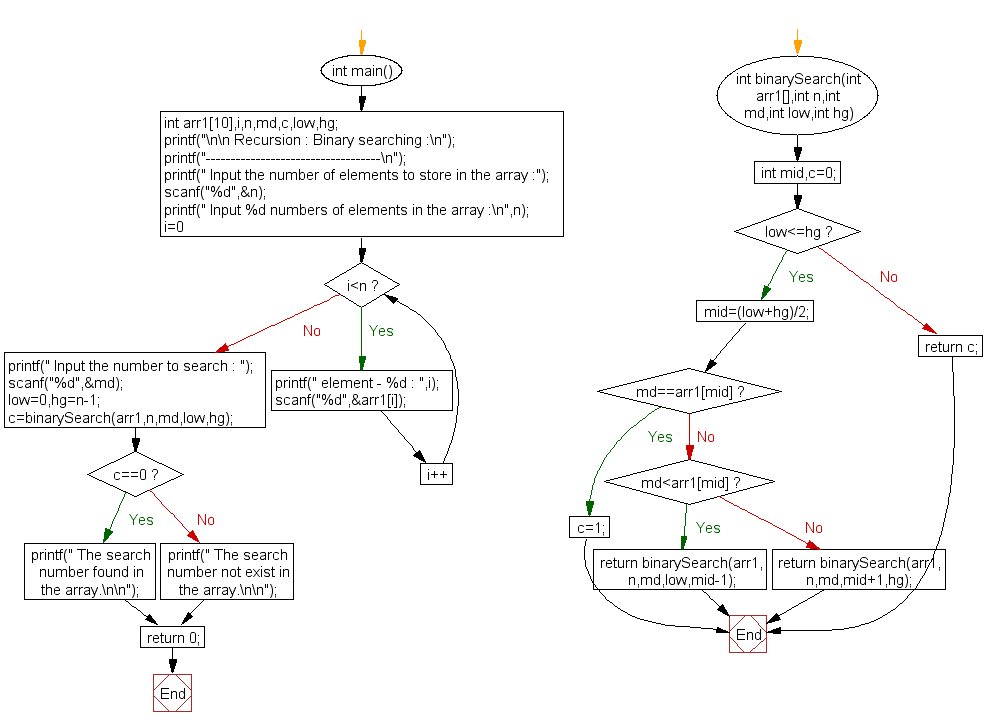
int binarySearch(int arr1[], int n, int md, int low, int hg)
{
    int mid, c = 0;
    if (low <= hg) 
    {
        mid = (low + hg) / 2;
        if (md == arr1[mid]) 
        {
            c = 1;
        }
        else if (md < arr1[mid]) 
        {
            return binarySearch(arr1, n, md, low, mid - 1);
        }
        else
            return binarySearch(arr1, n, md, mid + 1, hg);
    }
    else
        return c;
}

Sample Output:

 Input the number of elements to store in the array :3                                                        
 Input 3 numbers of elements in the array in ascending order :                                                
 element - 0 : 15                                                                                             
 element - 1 : 25                                                                                             
 element - 2 : 35                                                                                             
 Input the number to search : 35                                                                              
 The search number found in the array.

Explanation:

int binarySearch(int arr1[], int n, int md, int low, int hg)
{
    int mid, c = 0;
    if (low <= hg) 
    {
        mid = (low + hg) / 2;
        if (md == arr1[mid]) 
        {
            c = 1;
        }
        else if (md < arr1[mid]) 
        {
            return binarySearch(arr1, n, md, low, mid - 1);
        }
        else
            return binarySearch(arr1, n, md, mid + 1, hg);
    }
    else
        return c;
}

The function binarySearch () takes four arguments: the integer array arr1, the size of the array n, the element to search for md, and the lower and upper bounds of the search low and hg.

Inside the function, we first compute the middle index mid of the current search range.
We then compare the element at index mid with the target element md. If they are equal, we set a flag variable c to 1, indicating that we have found the element.
If the element at index mid is greater than the target element md, we recursively call the function on the lower half of the search range, i.e., from low to mid-1.
If the element at index mid is less than the target element md, we recursively call the function on the upper half of the search range, i.e., from mid+1 to hg.
If the lower bound low is greater than the upper bound hg, we have exhausted the search range without finding the element, so we return the flag variable c, which is still set to 0.

Time complexity and space complexity:

The time complexity of the binary search algorithm is O(log n), where n is the size of the array.

The space complexity of the recursive function is O(log n) due to the call stack.

Flowchart:

For more Practice: Solve these Related Problems:

Write a C program to implement binary search recursively on an array of strings using a custom comparator.
Write a C program to perform recursive binary search and count the number of comparisons made.
Write a C program to recursively search for the first occurrence of a target element in a sorted array with duplicates.
Write a C program to implement binary search recursively and return both the found index and the recursion depth.

C Programming Code Editor:

Previous: Write a program in C to find the first capital letter in a string using recursion.
Next: C File Handling Exercises Home