C++ Exercises: Find circular prime numbers upto a specific limit
31. Find Circular Primes Up to a Specific Limit
Write a C++ program to find circular prime numbers up to a specific limit.
Sample Solution:
C++ Code :
#include<iostream> // Including input-output stream header file
#include<cmath> // Including math functions
using namespace std; // Using standard namespace
int flg; // Flag variable used for prime number checking
// Function to check if a number is prime
void chkPrime(long int n)
{
long int i;
i = n - 1;
while (i>= 2) // Checking divisibility of the number
{
if (n % i == 0) // If number is divisible by i, set flag as 1 (not a prime number)
{
flg = 1;
}
i--;
}
}
// Function to generate all combinations of a number's digits
void AllCombination(long int a)
{
long int b, c, d, e, i, j, k, s, z, v, x[8], y[8], m; // Declaring variables
b = a;
i = 0;
while (b > 0) // Extracting digits from the number
{
y[i] = b % 10;
b = b / 10;
i++;
}
c = 0;
for (j = i - 1; j >= 0; j--) // Reversing the order of digits
{
x[c] = y[j];
c++;
}
m = i;
while (m > 0) // Generating circular combinations
{
c = m - 1;
d = i - 1;
e = 0;
s = 0;
while (e <i) // Creating circular combinations by rotating digits
{
z = pow(10, d);
v = z * x[c % i];
c++;
d--;
e++;
s = s + v;
}
m--;
chkPrime(s); // Checking if the generated combination is a prime number
}
}
// Main function
int main()
{
long int i = 2, ctr; // Initializing variables
// Prompting the user for input
cout<< "\n\n Find Circular Prime Numbers upto a specific limit: \n";
cout<< " ---------------------------------------------------\n";
cout<< " Enter the upper Limit: ";
cin>>ctr; // Reading upper limit from user
cout<< "\n The Circular Prime Numbers less than " <<ctr<< " are: " <<endl;
while (i<= ctr) // Loop to find circular prime numbers less than the upper limit
{
flg = 0; // Initializing flag variable
AllCombination(i); // Generating all combinations of the number
if (flg == 0) // If flag remains 0, the number is a circular prime
{
cout<<i<< " "; // Displaying circular prime number
}
i++;
}
cout<<endl;
return 0; // Returning from main function
}
OR
C++ Code:
#include <bits/stdc++.h> // Include standard library header
using namespace std; // Using standard namespace
// Sieve of Sundaram function to mark non-prime numbers
voidSieveOfSundaram(bool marked[], intnNew) {
for (inti = 1; i<= nNew; i++)
for (int j = i; (i + j + 2 * i * j) <= nNew; j++)
marked[i + j + 2 * i * j] = true;
}
// Function to rotate a number
int Rotate(int n) {
int rem = n % 10; // Finding the unit place number
rem *= pow(10, countDigits(n)); // Moving the unit place number to the front
n /= 10; // Removing the unit digit
n += rem; // Adding the first digit to the rest
return n;
}
// Function to count digits in a number
intcountDigits(int n) {
int digit = 0;
while (n /= 10)
digit++;
return digit;
}
// Function to find circular prime numbers within a range
voidcircularPrime(int n) {
intnNew = (n - 2) / 2;
bool marked[nNew + 1];
memset(marked, false, sizeof(marked)); // Initialize all values as false
SieveOfSundaram(marked, nNew); // Apply the Sieve of Sundaram
cout<< "2 "; // Start printing from number 2
for (inti = 1; i<= nNew; i++) {
if (marked[i] == true)
continue; // Skip marked numbers
intnum = 2 * i + 1; // Generate odd numbers
num = Rotate(num); // Rotate the number
while (num != 2 * i + 1) {
if (num % 2 == 0) // Check for even numbers
break; // Break the loop for even numbers
if (marked[(num - 1) / 2] == false)
num = Rotate(num); // Rotate non-marked numbers
else
break; // Break the loop for marked numbers
}
if (num == (2 * i + 1))
cout<<num<< " "; // Print circular prime numbers
}
}
// Main function
int main(void) {
int n = 100; // Define the upper limit
circularPrime(n); // Find circular prime numbers within the range
return 0; // Return from main function
}
Sample Output:
Find Circular Prime Numbers upto a specific limit:
---------------------------------------------------
Enter the upper Limit: 248
The Circular Prime Numbers less than 248 are:
2 3 5 7 11 13 17 31 37 71 73 79 97 113 131 197 199
Flowchart:
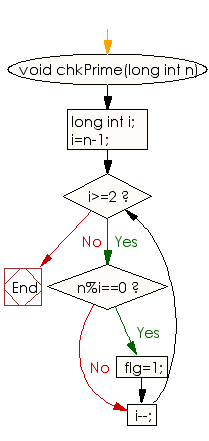
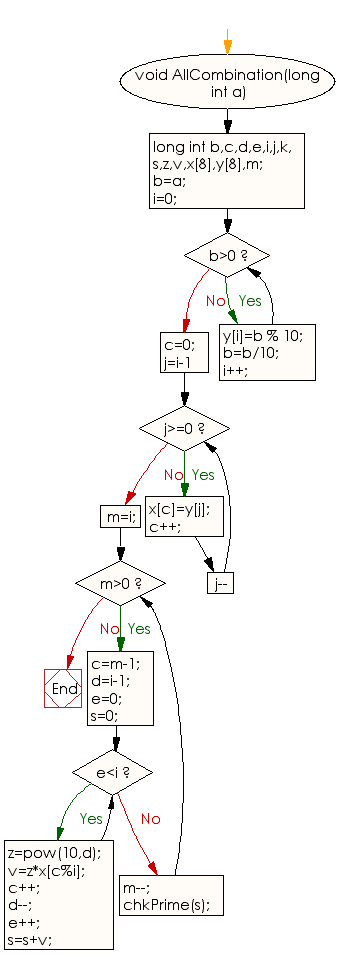
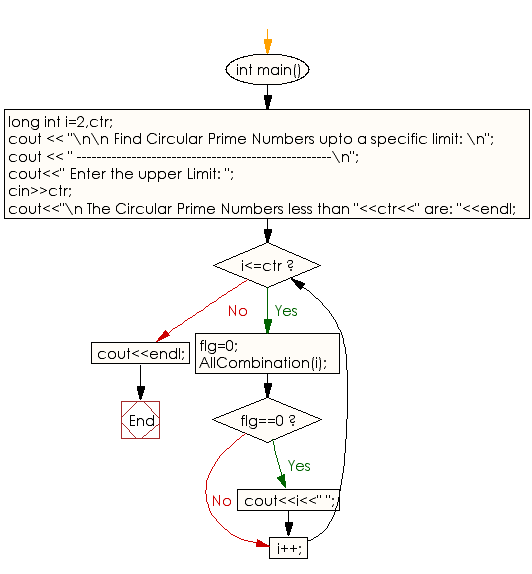
For more Practice: Solve these Related Problems:
- Write a C++ program to generate all circular primes below a given limit using iterative rotations.
- Write a C++ program to list circular primes in a range by combining prime sieving with digit rotation.
- Write a C++ program to find circular primes up to a specified limit with optimized prime checking routines.
- Write a C++ program to display circular primes by storing candidates in a vector and validating each rotation.
Go to:
PREV : Circular Prime Check.
NEXT : Perfect Cube Check.
C++ Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
