C++ Queue Exercises: Find the median of all elements of the said queue
6. Median of Queue Elements
Write a C++ program to find the median of all elements of a queue.
Sample Solution:
C Code:
#include <iostream>
#include <stack>
using namespace std;
const int MAX_SIZE = 100;
class Queue {
private:
int front; // Front index of the queue
int rear; // Rear index of the queue
int arr[MAX_SIZE]; // Array to store elements
public:
Queue() {
front = -1; // Initialize front index to -1
rear = -1; // Initialize rear index to -1
}
bool isFull() {
return (rear == MAX_SIZE - 1); // Check if the queue is full
}
bool isEmpty() {
return (front == -1 && rear == -1); // Check if the queue is empty
}
void enqueue(int x) {
if (isFull()) {
cout << "Error: Queue is full" << endl; // Display error message if queue is full
return;
}
if (isEmpty()) {
front = 0;
rear = 0;
} else {
rear++;
}
arr[rear] = x; // Insert the element at the rear index
}
void dequeue() {
if (isEmpty()) {
cout << "Error: Queue is empty" << endl; // Display error message if queue is empty
return;
}
if (front == rear) {
front = -1;
rear = -1;
} else {
front++;
}
}
int peek() {
if (isEmpty()) {
cout << "Error: Queue is empty" << endl; // Display error message if queue is empty
return -1;
}
return arr[front]; // Return the element at the front of the queue
}
void display() {
if (isEmpty()) {
cout << "Error: Queue is empty" << endl; // Display error message if queue is empty
return;
}
cout << "Queue elements are: ";
for (int i = front; i <= rear; i++) {
cout << arr[i] << " "; // Display all elements in the queue
}
cout << endl;
}
// Function to calculate the median of elements in the queue
float median_Queue(Queue & q) {
if (q.isEmpty()) {
cout << "Error: Queue is empty" << endl; // Display error message if queue is empty
return 0.0;
}
int count = 0;
int mid = 0;
for (int i = q.front; i <= q.rear; i++) {
count++; // Count the number of elements
}
mid = count / 2; // Calculate the middle index
if (count % 2 == 0) {
// If the count is even, calculate the average of two middle elements
float median = static_cast < float > (q.arr[q.front + mid] + q.arr[q.front + mid - 1]) / 2;
return median;
} else {
// If the count is odd, return the middle element
float median = q.arr[q.front + mid];
return median;
}
}
};
int main() {
cout << "Initialize a Queue." << endl;
Queue q;
cout << "\nInsert some elements into the queue:" << endl;
q.enqueue(1);
q.enqueue(2);
q.enqueue(3);
q.enqueue(4);
q.enqueue(5);
q.display();
// Calculate and display the median of elements in the queue
float med_val = q.median_Queue(q);
cout << "Find the median of all elements of the said queue: " << med_val;
cout << "\n\nInput one more element into the queue:" << endl;
q.enqueue(6);
q.display();
// Calculate and display the median of elements in the queue after adding a new element
med_val = q.median_Queue(q);
cout << "Find the median of all elements of the said queue: " << med_val;
return 0;
}
Sample Output:
Initialize a Queue. Insert some elements into the queue: Queue elements are: 1 2 3 4 5 Find the median of all elements of the said queue: 3 Input one more element into the queue: Queue elements are: 1 2 3 4 5 6 Find the median of all elements of the said queue: 3.5
Flowchart:
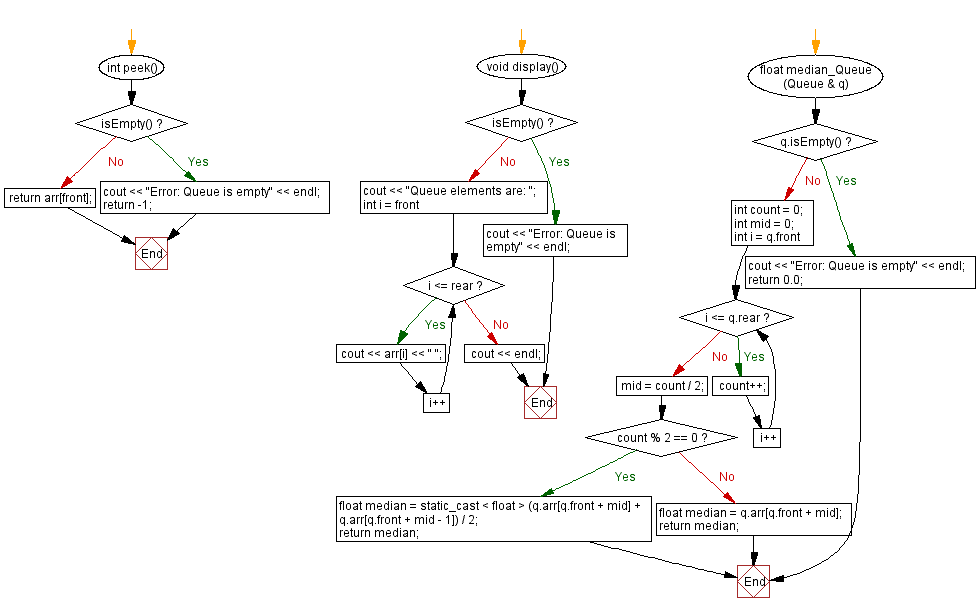
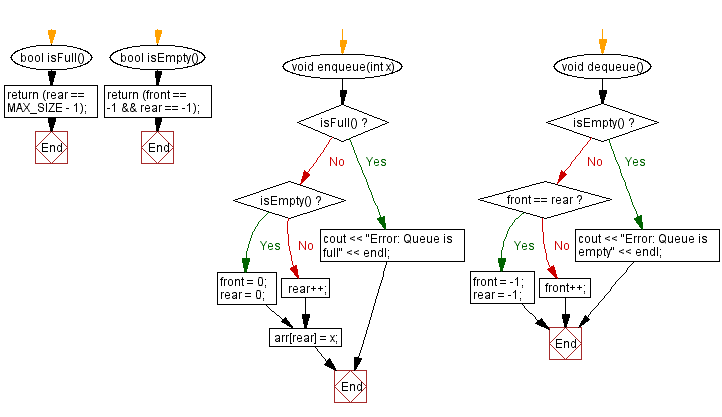
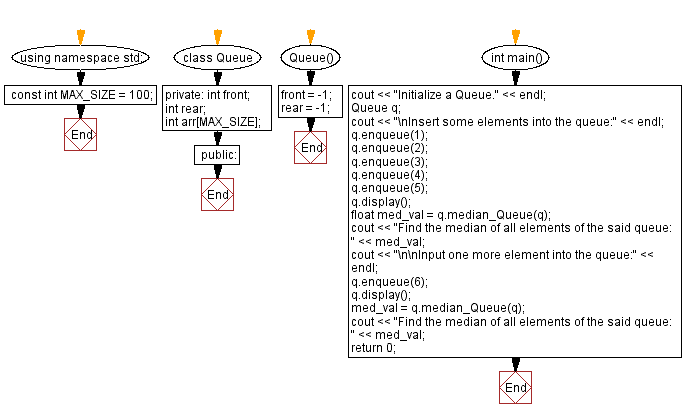
For more Practice: Solve these Related Problems:
- Write a C++ program to compute the median of a queue by first transferring its elements to a vector and sorting it.
- Write a C++ program to determine the median of a dynamically changing queue without altering the original order.
- Write a C++ program to calculate the median of queue elements using two heaps to maintain order.
- Write a C++ program to find the median of a queue in real-time as elements are enqueued and dequeued.
Go to:
PREV : Average of Queue Elements.
NEXT : Mode of Queue Elements.
CPP Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
