C#: Find the Sum of GP series
Write a C# Sharp program to find the sum of the Geometric Progress series.
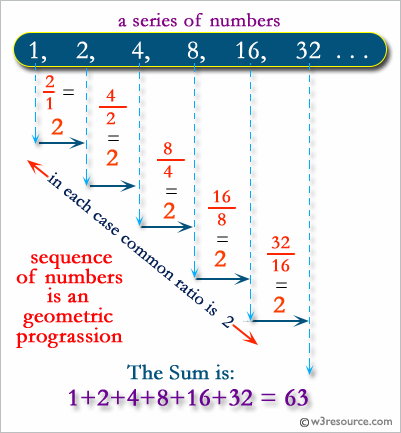
Sample Solution:-
C# Sharp Code:
using System; // Importing necessary namespace
public class Exercise52 // Declaration of the Exercise52 class
{
public static void Main() // Main method, entry point of the program
{
// Declaration of variables
int g1, cr, j;
int ntrm;
double sum = 0, tn, gpn;
// Displaying information about finding the sum of a GP series
Console.Write("\n\n");
Console.Write("Find the Sum of GP series:\n");
Console.Write("----------------------------");
Console.Write("\n\n");
// Prompting the user to input the first number, number of terms, and common ratio
Console.Write("Input the first number of the G.P. series: ");
g1 = Convert.ToInt32(Console.ReadLine());
Console.Write("Input the number of terms in the G.P. series: ");
ntrm = Convert.ToInt32(Console.ReadLine());
Console.Write("Input the common ratio of G.P. series: ");
cr = Convert.ToInt32(Console.ReadLine());
/*-------- generate G.P. series ---------------*/
Console.Write("\nThe numbers for the G.P. series:\n ");
Console.Write("1 "); // First term of the series
// Loop to generate the geometric progression (G.P.) series
for (j = 1; j <= ntrm; j++)
{
gpn = Math.Pow(cr, j); // Calculate each term of the series
Console.Write("{0} ", gpn); // Display the terms
}
/*-------- End of G.P. series generation ---------------*/
// Formula to calculate the sum of the G.P. series
sum = (g1 * (1 - (Math.Pow(cr, ntrm + 1)))) / (1 - cr);
tn = g1 * (Math.Pow(cr, ntrm - 1)); // Calculating the tn term of the G.P. series
// Displaying the tn term and the sum of the G.P. series
Console.Write("\nThe tn term of G.P. : {0}\n\n", tn);
Console.Write("\nThe Sum of the G.P. series : {0}\n\n", sum);
}
}
Sample Output:
Find the Sum of GP series: ---------------------------- Input the first number of the G.P. series: 1 Input the number or terms in the G.P. series: 5 Input the common ratio of G.P. series: 10 The numbers for the G.P. series: 1 10 100 1000 10000 100000 The tn terms of G.P. : 10000 The Sum of the G.P. series : 111111
Flowchart:
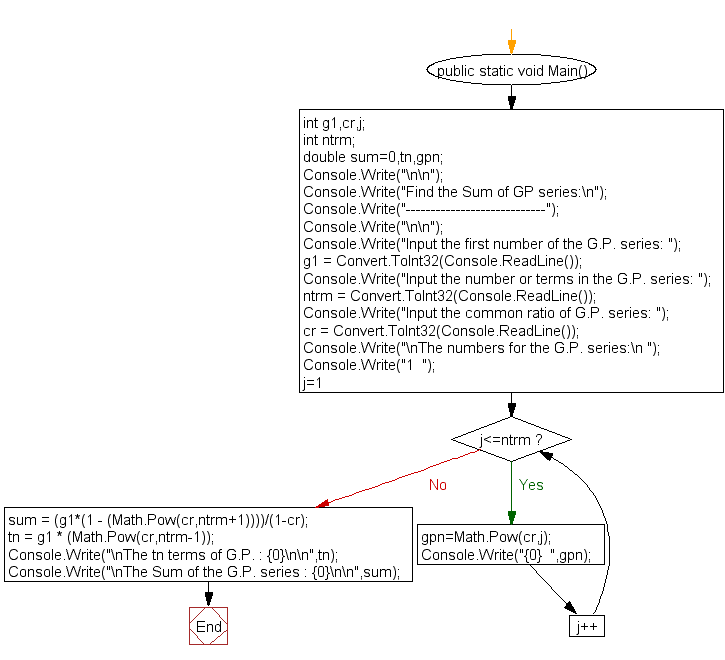
Go to:
PREV : Write a program in C# Sharp to convert a Octal number to Decimal number without using an array, function and while loop.
NEXT : Write a program in C# Sharp to convert a binary number to octal.
C# Sharp Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
