Solving the Two Sum Problem: Algorithms and Code Solutions

Two Sum

Given an array of integers, find two numbers such that they add up to a specific target.

• Input and Output Requirements
• Real-world Scenario
• Underlying Concepts
• Examples and Illustrations
• Brute Force Approach
• Optimization Techniques
• Algorithmic Thinking
• Algorithmic Strategies
• Common Mistakes and Pitfalls
• Coding Best Practices
• Testing and Debugging
• Algorithm Analysis
• Application in Real-world Projects
• Example test cases
• Solution for different languages
• Time and Space Complexity

Input and Output Requirements:

• Input:
An array of integers.
A specific target sum.
• Output:
Two numbers from the array that add up to the target.

Real-world Scenario:

Example-1:

Consider a scenario where you have a list of expenses over several days. The task is to find two days when the combined expenses equal a specific target amount. The array represents daily expenses, and the target is the desired total expense.

Daily Expenses: [20, 10, 5, 15, 25, 30]

Target Expense: 35

In this scenario:

• We want to find two days (represented by the array elements) where the combined expenses result in a total expense equal to the target (in this case, 35).
• The correct solution is to choose day 2 (10) and day 5 (25) since 10 + 25 = 35, which matches the target expense.

Example-2:

Imagine you have a list of prices for items in a store over several days. The task is to find two days when the prices of two items add up to a specific target amount. The array represents the prices of items, and the target is the desired total price.

Item Prices: [25, 30, 15, 10, 20, 35]

Target Price: 45

In this scenario:

• We want to find two days (represented by the array elements) when the prices of two items add up to the target (in this case, 45).
• Start with the first price, 25. The difference between the target price (45) and 25 is 20.
• Check if 20 exists in the prices that have been iterated through so far. It does, at index 4.
• So, the correct solution is to choose day 1 (25) and day 5 (20), as 25 + 20 = 45, which is the target price.

Underlying Concepts:

Sum and Complements:

The "Two Sum" problem involves finding two numbers in an array such that they add up to a specific target. To understand and solve this problem, we introduce the following key concepts:

• Sum and Target: The fundamental goal is to identify a pair of numbers in the array whose sum equals the specified target.
• Complements: To find two numbers that add up to the target, we utilize the concept of complements. The complement of a number a with respect to the target is (target - a).
• Basic Idea: For each element a in the array, if its complement (target - a) is present in the array, we have found our solution.

Examples and Illustrations:

Walkthrough Examples:

Example 1:

• Consider the array [2, 7, 11, 15] and the target sum 9.
• Start with the first element 2.
• Check if the complement (target - 2) is present in the array. Here, it is 7, and it is present.
• We found a pair (2, 7) that adds up to the target 9.

Example 2:

Take the array [3, 5, 8, 2, 10] and the target sum 13.

• Begin with the first element 3.
• Check if the complement (target - 3) is present. Here, it is 10, and it is in the array.
• We found a pair (3, 10) that adds up to the target 13.

Visualization:

Here are some key characteristics and additional details:

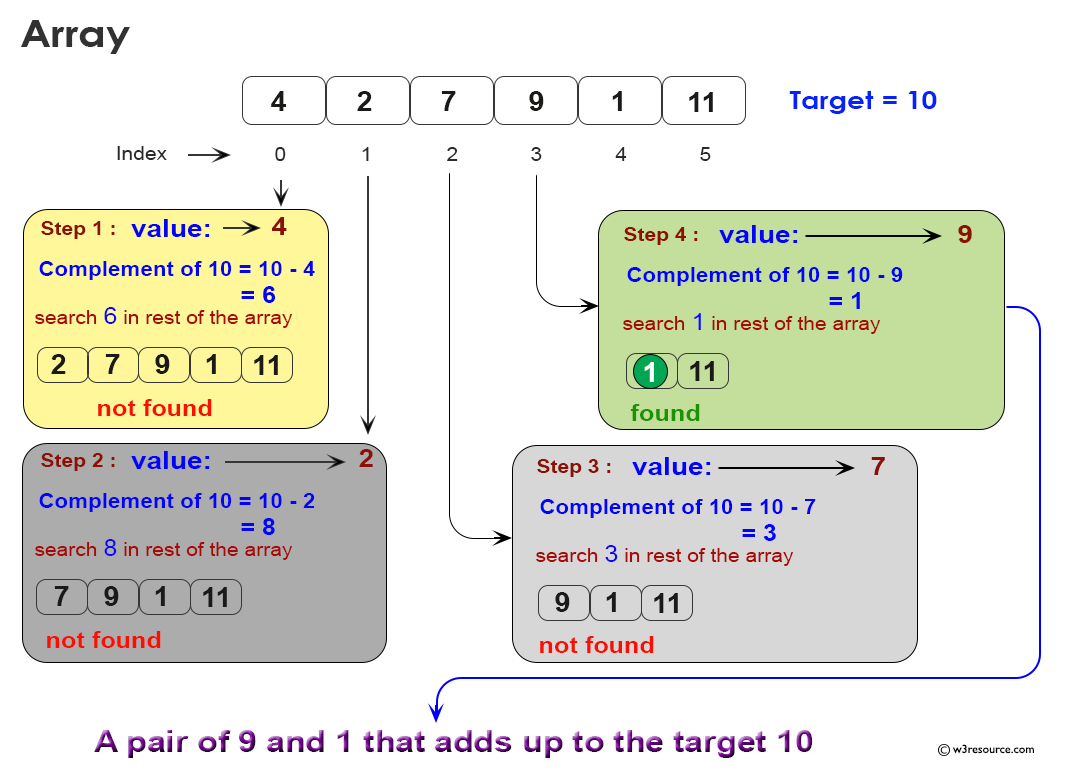
In this visualization, we see the process of iterating through the array, checking complements, and searching for a pair that adds up to the target 10. This visual representation helps in understanding the step-by-step approach to solving the problem.

Brute Force Approach:

The Brute Force Approach is a straightforward and exhaustive algorithmic technique that involves checking all possible solutions to a problem. This is done to find the one that meets the criteria.

Naive Solution:

The brute force approach for the "Two Sum" problem involves checking all possible pairs of numbers in the array to find the ones that add up to the given target. The steps include:

• Nested Loop:
• Iterate through each element in the array using a nested loop.
• For each element arr[i], iterate through the remaining elements arr[j] (where j > i).
• Pair Sum Check:
• Check if the sum of the current pair (arr[i], arr[j]) equals the target.
• If a pair with the target sum is found, return the indices or values of the pair.
• Complete Search:
• Continue this process until all pairs are checked or a pair with the target sum is found.

Complexity Analysis:

Discuss the time and space complexity of the brute force approach.

• Time complexity:
• The nested loop structure results in a time complexity of O(n^2), where 'n' is the array size.
• For each element, we compare it with every other element, leading to quadratic time complexity.
• Space complexity:
• The space complexity is O(1) since we don't use additional data structures proportional to the input size.
• Efficiency:
• While this approach is straightforward, it may not be efficient for large datasets due to its quadratic time complexity.
• It involves redundant checks as pairs are examined multiple times.
• Use Cases:
• The brute force approach is practical for small datasets or when optimization is not a primary concern.
• It serves as a baseline solution but may be impractical for larger datasets or real-time applications.

Optimization Techniques:

The Hash Table Approach:

• Introduction:
• The Hash Table approach involves using a data structure that allows for efficient lookup of elements based on their keys.
• The key idea is to iterate through the array only once, storing each element's index and complement in the hash table.
• Steps:
• Iterate through the array.
• For each element arr[i], calculate its complement as (target - arr[i]).
• Check if the complement exists in the hash table.
• If found, return the indices of the two elements that add up to the target.
• Hash table benefits:
• Hash tables provide constant-time average-case complexity for lookups.
• Efficiently determines the existence of a complement, reducing redundant checks.

Complexity analysis:

• Time complexity:
• The time complexity is O(n) for the Hash Table approach.
• Iterating through the array once and checking the hash table for each element.
• Space complexity:
• Space complexity is O(n) for the Hash Table approach.
• Additional space is required for storing elements and their indices in the hash table.
• Comparison with Brute Force:
• The Hash Table approach is more efficient than the brute force approach for large datasets.
• Reduces time complexity from O(n^2) to O(n).
• Introduces additional space and complexity due to the hash table.
• Reduction in time complexity: By using a Hash Table, we can reduce time complexity from O(n^2) to O(n). This reduction is achieved by eliminating the need for nested loops that characterize the brute force approach. Instead, the Hash Table allows constant-time lookups, which improves overall efficiency.
• Additional space and complexity: While the Hash Table approach offers superior time complexity, it introduces additional space complexity due to the storage of key-value pairs in the hash table. This introduces some overhead in terms of memory usage and requires additional code complexity for handling hash collisions, resizing, etc. However, in most cases, the trade-off between time and space complexity favors the Hash Table approach, especially when dealing with large datasets.
• Trade-offs:
• While offering a significant improvement in time complexity, the hash table approach comes with increased space complexity.
• It strikes a balance between time and space efficiency, often preferred for larger datasets.
• Use cases:
• Suitable for scenarios where optimizing time complexity is crucial.
• Commonly used in practice due to its efficiency for moderate to large datasets.

Algorithmic Thinking:

Divide and Conquer:

• Breaking Down the Problem:
• Divide and Conquer involves breaking down a complex problem into simpler subproblems.
• For the "Two Sum" problem, the initial complexity can be overwhelming, but by breaking it into smaller steps, it becomes more manageable.
• Steps for Divide and Conquer:
• Identify key subproblems within the problem statement.
• Solve each subproblem independently.
• Combine the solutions of subproblems to obtain the overall solution.
• Application to "Two Sum":
• Identify the subproblems:
• Finding a pair in a smaller array that adds up to a specific target.
• Combining the results of smaller subproblems to get the final solution.
• Effectiveness:
• Divide and Conquer is effective when the problem can be easily divided into smaller, more manageable parts.
• Each subproblem is solved independently, simplifying the overall problem-solving process.

Algorithmic Strategies:

• Introduction:
• Algorithmic strategies involve adopting specific techniques or approaches to tackle problems more efficiently.
• In the context of "Two Sum," strategies like using complements and hash tables are algorithmic approaches.
• Using Complements:
• Recognizing that finding two numbers with a specific sum is equivalent to finding one number and its complement.
• This simplifies the problem, allowing for a more straightforward search.
• Hash Tables:
• Hash tables offer a strategy for optimizing the solution by trading space for time.
• Efficiently store elements and their indices, facilitating quick lookups.
• Algorithmic Efficiency:
• Algorithmic strategies aim to improve the efficiency of solving problems.
• Complements and hash tables provide alternative approaches that reduce time complexity.
• Adaptability:
• Algorithmic strategies adapt to various problem scenarios.
• They can be applied to different problems by leveraging the underlying principles.
• Problem-Specific Strategy:
• The choice of strategy depends on the problem requirements and constraints.
• Understanding the problem's nature guides the selection of the most appropriate strategy.

Common Mistakes and Pitfalls:

• Edge Cases:
• Overlooking the Empty Array:
• Mistake: Assuming the array always has elements.
• Solution: Check for an empty array at the beginning and handle it appropriately to avoid errors.
• Handling Single Element Array:
• Mistake: Not considering the case where the array has only one element.
• Solution: Ensure the algorithm works correctly for arrays with one or two elements.
• Extreme values:
• Mistake: Ignoring edge cases with extreme values (e.g., very large or very small integers).
• Solution: Test the algorithm with extreme values to verify its robustness.
• Handling Duplicate Pairs:
• Ignoring duplicate pairs:
• Mistake: Overlooking the possibility of duplicate pairs in the array.
• Solution: Account for duplicate pairs and decide whether to include them in the result or not.
• Counting the Same Elements Twice:
• Mistake: Counting the same element twice when considering pairs.
• Solution: Implement a mechanism to avoid pairing an element with itself.
• Handling reverse pairs:
• Mistake: Treating (a, b) and (b, a) as different pairs.
• Solution: Ensure symmetry in pairs, and handle reverse pairs appropriately.
• Zero as a Target:
• Missing Zero as a Target:
  • Mistake: Not testing the algorithm with a target of zero.
  • Solution: Explicitly test the algorithm with a target of zero to verify correctness.
• Overflow and Underflow:
• Ignoring integer overflow:
• Mistake: Not considering the possibility of integer overflow when calculating sums.
• Solution: Use data types that can handle large sums or implement checks to prevent overflow.
• Underestimating the Data Range:
  • Mistake: Assuming the data range is within a certain limit.
  • Solution: Be mindful of the potential range of data and choose appropriate data types.
• Handling Negative Numbers:
• Misinterpreting negative numbers:
• Mistake: Misinterpreting how negative numbers contribute to the target.
• Solution: Understand the impact of negative numbers on the target and adjust the algorithm accordingly.

Coding Best Practices:

• Modularity:
• Emphasizing the modular code:
• Break down the solution into modular functions or methods, each addressing a specific subtask.
• Encapsulate logic related to specific functionalities within dedicated functions.

• Advantages of modularity:
• Improved readability: Each function focuses on a specific task, making the code easier to understand.
• Reusability: Modular functions can be reused in other parts of the code or in different projects.
• Easy debugging: Isolate and troubleshoot issues in specific modules without affecting the entire codebase.

• Example (Python code):

 def find_two_sum(nums, target):
    # Function for finding two numbers that add up to the target
    # ...

def main():
    # Main function to orchestrate the program
    # ...

if __name__ == "__main__":
    main()

• The Importance of Meaningful Names:
• Choose descriptive and meaningful variable names that convey the purpose or content of the variable.
• Avoid single-letter variable names unless they represent common conventions (e.g., loop indices).

• Benefits of Good Variable Naming:
• Readability: Clear and descriptive names enhance code readability for yourself and others.
• Maintenance: Easier maintenance as the purpose of variables is evident.
• Reduced comments: Well-named variables can reduce the need for excessive comments.

• Example (Python code)

 def find_two_sum(nums, target):
    # nums: Input array of integers
    # target: Specific target sum
    for index, num in enumerate(nums):
        complement = target - num
        # ...

• Consistent coding style:
• Maintain a consistent coding style throughout the codebase.
• Follow established conventions, such as PEP 8 for Python, for a uniform appearance.

• Version Control and Collaboration:
• Consistency facilitates version control and collaboration, especially in team environments.
• Adopting a consistent style ensures that team members can easily understand and contribute to the code.

• Example (Python code):

# Inconsistent Style
def findTwoSum(nums, target):
    for i, n in enumerate(nums):
        complement = target - n
        # ...

# Consistent Style (Following PEP 8)
def find_two_sum(nums, target):
    for i, num in enumerate(nums):
        complement = target - num
        # ...

Testing and Debugging:

Test cases:

• Test Case Selection:
• Test the solution with a variety of input scenarios to ensure its correctness.
• Include both typical cases and edge cases to cover a wide range of possibilities.
• Example Test Cases for "Two Sum":
• Positive cases with valid pairs that sum up to the target.
• Negative cases with no valid pairs.
• Cases with a target of zero.
• Edge cases with empty arrays, single-element arrays, and extreme values.
• Test Case Execution:
• Automate the execution of test cases to streamline the testing process.
• Use testing frameworks or write custom test scripts to cover various scenarios.

Debugging techniques:

• Print Statements:
• Insert print statements strategically to output variable values and intermediate results.
• Helps identify where the code deviates from the expected behavior.
• Use a debugger:
• Utilize integrated development environment (IDE) debuggers to set breakpoints and step through the code.
• Inspect variable values and control flow to pinpoint issues.
• Code Review:
• Engage in code reviews with peers or mentors.
• External perspectives can reveal overlooked errors or suggest alternative approaches.
• Rubber Duck Debugging:
• Explain the code step by step to an inanimate object (or a colleague).
• The act of verbalizing often helps in identifying logical errors.
• Isolated Sections:
• Temporarily comment out or isolate specific sections of code to identify the source of errors.
• Narrow down the scope of investigation to smaller segments.
• Check variable values:
• Ensure that variables hold expected values at different stages of execution.
• Pay attention to changes in variable states.
• Use exception handling:
• Implement exception handling to catch and log errors.
• This prevents the program from crashing abruptly, providing information about the error.
• Reproduce the Issue:
• Try to reproduce the issue in a controlled environment.
• Identify the steps leading to the error and examine the relevant code.
• Logging:
• Incorporate logging statements to record the program's state during execution.
• Log messages provide insights into the program flow and variable values.
• Test incrementally:
• Implement and test the solution incrementally, focusing on small sections at a time.
• Detect issues early in the development process.
• Pair Programming:
• Collaborate with a partner in a pair programming session.
• Two sets of eyes can catch errors more effectively.

Algorithm Analysis:

• Time and Space Complexity:
• Time Complexity Analysis:
• Evaluate the efficiency of the algorithm in terms of input size.
• Identify the dominant operations and quantify their relationship with input size.
• Example (Two Sum):
• For the Hash Table approach, iterating through the array once results in a time complexity of O(n).
• Hash table lookups are typically O(1) on average, making the overall time complexity O(n).

• Space Complexity Analysis:
• Assess the algorithm's memory usage in relation to input size.
• Consider additional data structures and their impact on space complexity.

• Example (Two Sum):
• The Hash Table approach requires O(n) space to store elements and indices.

• Trade-offs:
• Time vs. Space Complexity:
• Evaluate the trade-offs between optimizing for time or space.
• Some algorithms prioritize reduced time complexity, while others prioritize minimal space usage.
• Example Trade-off (Two Sums):
• The Brute Force approach has higher time complexity (O(n^2)) but minimal space complexity (O(1)).
• The Hash Table approach has improved time complexity (O(n)) but higher space complexity (O(n)).
• Memory Efficiency vs. Speed:
• Consider the balance between memory efficiency and algorithmic speed.
• Optimize the algorithm based on the specific requirements and constraints of the problem.
• Example Trade-off (Two Sum):
• The Hash Table approach sacrifices space efficiency for faster lookup times.
• In scenarios with limited memory, an alternative approach might be preferred.
• Algorithmic Strategies:
• Choose algorithmic strategies based on the problem's characteristics and constraints.
• Select an approach that aligns with the specific goals of the application.
• Example Trade-off (Two Sum):
• The choice between Brute Force and Hash Table approaches depends on the size of the input array and the available memory.
• For small arrays, the Brute Force approach may be sufficient, while the Hash Table approach is more suitable for larger datasets.
• Scalability:
• Consider how well the algorithm scales as the input size increases.
• Choose an algorithm that maintains efficiency with growing datasets.
• Example Trade-off (Two Sum):
• The Hash Table approach is more scalable for larger arrays, as its time complexity grows linearly with input size.

Application in Real-world Projects:

• Practical Use Cases:
• Financial Transactions:
• Scenario: In financial systems, detecting fraudulent transactions often involves identifying unusual behavior patterns.
• Algorithmic Approach: Two Sum algorithms can be employed to efficiently search for pairs of transactions with suspiciously high or low values.
• Stock Market Analysis:
• Scenario: Analyzing historical stock prices to identify days when the sum of prices meets specific criteria.
• Algorithmic Approach: A Two Sum approach can help find pairs of days with desired stock price patterns.
• Network Security:
• Scenario: Detecting network anomalies by identifying pairs of events indicating potential security threats.
• Algorithmic Approach: Similar to financial transactions, Two Sum algorithms can assist in recognizing unusual network patterns.
• Supply Chain Optimization:
• Scenario: In supply chain management, identifying pairs of products whose demand, when combined, matches specific criteria.
• Algorithmic Approach: Two Sum algorithms can be used to efficiently search for such pairs, aiding in inventory planning.
• Social Network Recommendations:
• Scenario: Recommending connections or friends based on shared interests or activities.
• Algorithmic Approach: Two Sum algorithms can help identify pairs of users with similar preferences or activities.
• Further Exploration:
• Exploring Additional Challenges:
• Encourage learners to explore variations of the Two Sum problem, such as finding three numbers that add up to a target. In addition, learners can handle negative numbers.
• Challenge them to adapt the solution to different use cases or constraints.
• Algorithmic Variations:
• Explore algorithms beyond Two Sum, such as Three Sum, where the task is to find three numbers that add up to a specific target.
• Consider variations that involve multiple constraints, like finding pairs with a maximum or minimum difference.

Example test cases:

• Positive cases with valid pairs that sum up to the target:
• Input: nums = [2, 7, 11, 15], target = 9 Expected output: [0, 1] (as 2 + 7 = 9)
• Input: nums = [3, 2, 4], target = 6 Expected output: [1, 2] (as 2 + 4 = 6)
• Negative cases with no valid pairs:
• Input: nums = [3, 5, 8, 2], target = 20 Expected output: [] (no pairs add up to 20)
• Input: nums = [-1, -2, -3, -4, -5], target = -10 Expected output: [] (no pair adds up to -10)
• Cases with a target of zero:
• Input: nums = [0, 1, 2, 3, 4, 5], target = 0 Expected output: []. According to the problem statement, the Two Sum problem requires finding two distinct numbers in the array that sum up to the target. The expected output should be an empty array [] because there are no distinct numbers in the array that can be added to get the target of 0.
• Input: nums = [], target = 0 Expected output: [] (empty array)
• Edge cases with empty arrays, single-element arrays, and extreme values:
• Input: nums = [], target = 5, Expected output: [] (empty array)
• Input: nums = [5], target = 5, Expected output: [] (single-element array)
• Input: nums = [1000000000, -1000000000, 2000000000, -2000000000], target = 0 Expected output: [1, 0] (as -1000000000 + 1000000000 = 0)

Solution for different languages:

Python - Array Two Sum Solution:

Code:

def two_sum(nums, target):
    # Create an empty dictionary to store numbers and their indices
    num_dict = {}
    
    # Iterate through each number and its index in the input list
    for i, num in enumerate(nums):
        # Calculate the complement of the current number with respect to the target
        complement = target - num
        
        # Check if the complement exists in the dictionary
        if complement in num_dict:
            # If complement exists, return the indices of the two numbers that add up to the target
            return [num_dict[complement], i]
        
        # If complement doesn't exist, add the current number and its index to the dictionary
        num_dict[num] = i
    
    # If no such pair is found, return an empty list
    return []


# Example usage:
nums = [20, 10, 5, 15, 25, 30]
target = 35
print(two_sum(nums, target))  # Output: [0, 3]
 
nums = [-1, -2, -3, -4, -5]
target = -10
print(two_sum(nums, target))  # Output: [] (no pair adds up to -10)

nums = []
target = 0 
print(two_sum(nums, target))  # Output: [] (empty array)

nums = [5]
target = 5
print(two_sum(nums, target))  # Output: [] (single-element array)

nums = [1000000000, -1000000000, 2000000000, -2000000000]
target = 0 
print(two_sum(nums, target)) # Output: [0, 1]

Output:

[0, 3]
[]
[]
[]
[0, 1]

Explanation of the said Python code:

• Function Definition:
• The "two_sum()" function takes two arguments: 'nums', which is a list of integers, and 'target', which is the desired sum of two numbers.
• Initialization:
• The function initializes an empty dictionary called 'num_dict'. This dictionary will be used to store numbers encountered in the input list and their corresponding indices.
• Iteration through the input list:
• The function iterates through each element 'num' and its index 'i' in the 'nums' list using the "enumerate()" function.
• Calculating the complement:
• For each 'num', the code calculates the complement by subtracting 'num' from the 'target'. The complement represents the value that, when added to 'num', will result in the target sum.
• Checking for complement in the Dictionary:
• The code checks if the complement exists in the 'num_dict' dictionary. If the complement is found in the dictionary, it means that a pair of numbers has been found whose sum equals the target.
• If the complement exists, the function immediately returns a list containing the indices of the two numbers (the index of the complement stored in the dictionary and the current index 'i').
• Storing Number-Index Pairs in a Dictionary:
• If the complement does not exist in the dictionary, the current number 'num' and its index 'i' are added to 'num_dict'. This allows the function to keep track of the numbers encountered so far.
• Return values:
• If no pair of numbers is found that adds up to the target, the function returns an empty list [].

Java - Array Two Sum Solution

Code:

// Importing necessary Java utilities
import java.util.HashMap;
import java.util.Map;

// Definition of the TwoSum class
public class TwoSum {

    // Method to find two numbers in the array that add up to the target
    public int[] twoSum(int[] nums, int target) {
        // Creating a HashMap to store numbers and their indices
        Map<Integer, Integer> numMap = new HashMap<>();

        // Iterating through the array
        for (int i = 0; i < nums.length; i++) {
            // Calculating the complement for the current number
            int complement = target - nums[i];

            // Checking if complement exists in the HashMap
            if (numMap.containsKey(complement)) {
                // If complement exists, return the indices of the two numbers
                return new int[]{numMap.get(complement), i};
            }

            // Storing the current number and its index in the HashMap
            numMap.put(nums[i], i);
        }

        // If no such pair is found, return an empty array
        return new int[0];
    }

    // Main method for testing the TwoSum class
    public static void main(String[] args) {
        // Creating an instance of the TwoSum class
        TwoSum twoSum = new TwoSum();

        // Input array and target sum
        int[] nums = {20, 10, 5, 15, 25, 30};
        int target = 35;

        // Finding the indices of the two numbers that add up to the target
        int[] result = twoSum.twoSum(nums, target);

        // Printing the indices of the two numbers
        for (int num : result) {
            System.out.print(num + " ");
        }
        // Output: 0 3
    }
}

Output:

0 3

Explanation of the said Java code:

• Importing Libraries: The code begins by importing the necessary Java utility classes (HashMap and Map) for storing key-value pairs.
• TwoSum Class Definition: The "TwoSum" class encapsulates the functionality to find the two numbers.
• twoSum Method: This method takes an array of integers ('nums') and a target sum ('target') as input and returns an array containing the indices of the two numbers that add up to the target sum. It utilizes a HashMap ('numMap') to store the numbers and their corresponding indices.
• Inside the method, it iterates through the 'nums' array.
• For each element 'num' in the array, it calculates the complement (the difference between 'target' and 'num').
• It checks if the complement exists in the 'numMap'. If it does, it returns the indices of the current element and the complement found in the 'numMap'.
• If the complement does not exist in the 'numMap', it adds the current element and its index to the 'numMap'.
• If no such pair is found, it returns an empty array.
• main Method: This method is used for testing the "twoSum()" method. It creates an instance of the "TwoSum" class, defines an input array 'nums', and a target sum 'target'. It then calls the "twoSum()" method with these inputs and prints the indices of the two numbers that add up to the target sum.

C++ - Array Two Sum Solution

Code:

#include <iostream>
#include <vector>
#include <unordered_map>

class Solution {
public:
    std::vector<int> twoSum(std::vector<int>& nums, int target) {
        std::unordered_map<int, int> numMap;
        for (int i = 0; i < nums.size(); ++i) {
            int complement = target - nums[i];
            if (numMap.find(complement) != numMap.end()) {
                return {numMap[complement], i};
            }
            numMap[nums[i]] = i;
        }
        return {};
    }
};

// Example usage:
int main() {
    Solution solution;
    std::vector<int> nums = {20, 10, 5, 15, 25, 30};
	    int target = 35;
    std::vector<int> result = solution.twoSum(nums, target);
    for (int num : result) {
        std::cout << num << " ";
    }
    // Output: 0 3
    return 0;
}

Output:

0 3

Explanation of the said C++ code:

• The "Solution" class contains a method "twoSum()" that takes a vector of integers 'nums' and an integer 'target' as input and returns a vector of integers representing the indices of the two numbers that sum up to the target.
• Inside the twoSum method:
• An unordered map 'numMap' is used to store the elements of the array 'nums' along with their indices for efficient lookup.
• The method iterates through the elements of 'nums' using a for loop.
• For each element 'nums[i]', it calculates the complement (the number needed to reach the target) as target - nums[i].
• If the complement exists in 'numMap', it means the current element and its complement add up to the target. The method returns the indices of the current element and its complement.
• If the complement does not exist in 'numMap', the current element and its index are added to 'numMap'.
• If no valid pair is found after iterating through all elements, an empty vector is returned.
• In the main function:
• An instance of the "Solution" class is created.
• A sample vector 'nums' and a target integer are defined.
• The "twoSum()" method is called with 'nums' and 'target', and the result is stored in the vector 'result'.
• The indices of the two numbers are printed out.

This code efficiently finds a pair of numbers in the array 'nums' that sum up to the target value.

C# - Array Two Sum Solution

Code:

using System;
using System.Collections.Generic;

public class Solution
{
    public int[] TwoSum(int[] nums, int target)
    {
        Dictionary<int, int> numMap = new Dictionary<int, int>();
        for (int i = 0; i < nums.Length; i++)
        {
            int complement = target - nums[i];
            if (numMap.ContainsKey(complement))
            {
                return new int[] { numMap[complement], i };
            }
            numMap[nums[i]] = i;
        }
        return new int[0];
    }

    static void Main(string[] args)
    {
        Solution solution = new Solution();
        int[] nums = { 20, 10, 5, 15, 25, 30 };
        int target = 35;
        int[] result = solution.TwoSum(nums, target);
        foreach (int num in result)
        {
            Console.Write(num + " ");
        }
        // Output: 0 3
    }
}

Output:

0 3

Explanation of the said C# code:

• The "Solution" class contains a method "TwoSum()" that takes an array of integers 'nums' and an integer 'target' as input and returns an array of integers representing the indices of the two numbers that sum up to the target.
• Inside the TwoSum method:
• A Dictionary<int, int> named 'numMap' is used to store the elements of the array 'nums' along with their indices for efficient lookup.
• The method iterates through the elements of 'nums' using a for loop.
• For each element 'nums[i]', it calculates the complement (the number needed to reach the target) as 'target - nums[i]'.
• If the complement exists in 'numMap' as a key, it means the current element and its complement add up to the target. The method returns the indices of the current element and its complement.
• If the complement does not exist in 'numMap', the current element and its index are added to 'numMap'.
• If no valid pair is found after iterating through all elements, an empty integer array is returned.
• In the Main method:
• An instance of the Solution class is created.
• A sample array nums and a target integer are defined.
• The TwoSum method is called with nums and target, and the result is stored in the array result.
• The indices of the two numbers are printed out using a foreach loop.

This code effectively finds a pair of numbers in the array nums that sum up to the target value.

JavaScript - Array Two Sum Solution

Code:

var twoSum = function(nums, target) {
    const numMap = new Map();
    for (let i = 0; i < nums.length; i++) {
        const complement = target - nums[i];
        if (numMap.has(complement)) {
            return [numMap.get(complement), i];
        }
        numMap.set(nums[i], i);
    }
    return [];
};

// Example usage:
const nums = [20, 10, 5, 15, 25, 30];
const target = 35;
console.log(twoSum(nums, target)); // Output: [0, 3]

Output:

[0, 3]

Explanation of the said JavaScript code:

• The "twoSum()" function takes an array 'nums' and a target integer 'target' as input and returns an array containing the indices of the two numbers that sum up to the target.
• Inside the twoSum function:
• It initializes a new "Map" object named 'numMap' to store elements of the array along with their indices for efficient lookup.
• It iterates through the elements of the array 'nums' using a "for" loop.
• For each element 'nums[i]', it calculates the complement (the number needed to reach the target) as 'target - nums[i]'.
• If the complement exists in 'numMap' as a key, it means the current element and its complement add up to the target. The function returns an array containing the indices of the current element and its complement.
• If the complement does not exist in 'numMap', the current element and its index are added to 'numMap' using the "set()" method.
• If no valid pair is found after iterating through all elements, an empty array is returned.
• Example usage:
• An array 'nums' and a target integer 'target' are defined.
• The "twoSum()" function is called with 'nums' and 'target', and the result is logged to the console.
• The output is the array [0, 3], indicating that the elements at indices 0 and 3 in the 'nums' array sum up to the target value of 35.

This code efficiently finds a pair of numbers in the 'nums' array that sum up to the target value.

Time and Space Complexity:

Time Complexity:

• The time complexity of the "twoSum()" method primarily depends on the size of the input array 'nums'.
• Inside the method, there is a loop that iterates through each element of the array once, resulting in a time complexity of O(n), where n is the length of the input array.
• Additionally, for each element, there is a constant-time operation of checking if the complement exists in the HashMap and putting the current number and its index in the HashMap.
• Therefore, the overall time complexity of the "twoSum()" method is O(n), where n is the length of the input array 'nums'.

Space Complexity:

• The space complexity of the "twoSum()" method is influenced by the extra space used to store elements in the HashMap.
• In the worst-case scenario, where no pair of numbers adds up to the target, the HashMap could store all elements of the input array along with their indices.
• Therefore, the space complexity of the "twoSum()" method is O(n), where n is the length of the input array 'nums', as it requires additional space proportional to the size of the input array.