Find the Missing Number: Algorithm Explanation

Last update on May 09 2024 09:37:38 (UTC/GMT +8 hours)

Problem Statement:

Find the Missing Number:

Given an array containing n distinct numbers taken from 0, 1, 2, ..., n, find the one missing from the array.

Input and Output Requirements
Real-world Scenario
Underlying Concepts
Examples and Illustrations
Brute Force Approach
Optimization Techniques
Algorithmic Thinking
Algorithmic Strategies
Common Mistakes and Pitfalls
Coding Best Practices
Testing and Debugging
Algorithm Analysis
Application in Real-world Projects
Example test cases
Solution for different languages
Time and Space Complexity

Input and Output Requirements:

Input: An array of distinct integers from 0 to n with one missing number.
Output: The missing number from the array.

Real-world Scenario:

Suppose a teacher distributes numbered assignments to students in a class, starting from 1 to n. Each student is assigned a unique number. However, one student misplaces or forgets to collect their assignment. In this situation, the teacher needs to identify the missing assignment number to follow up with it.

Underlying Concepts:

Array Indexing:

Arrays are indexed collections of elements, where each element is accessed using its index. In most programming languages, array indexing starts from 0. For example, in an array 'arr', 'arr[0]' represents the first element, 'arr[1]' represents the second element, and so on.

Mathematical Concepts:

Introduction:

Data Structure: DSA Missing Numbers Mathemetical concepts

Relationship with the Array: In the problem, the array consists of distinct numbers from 0 to n, where one number is missing. By calculating the sum of the first n natural numbers using the formula mentioned above and subtracting the sum of the elements in the array, the missing number can be determined.

Missing number:

When a number is missing from the array, it disrupts the expected sequence of numbers from 0 to n. This missing number directly impacts the total sum of the array. The goal of the problem is to identify this missing number by understanding its effect on the total sum of the array.

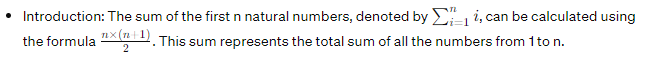
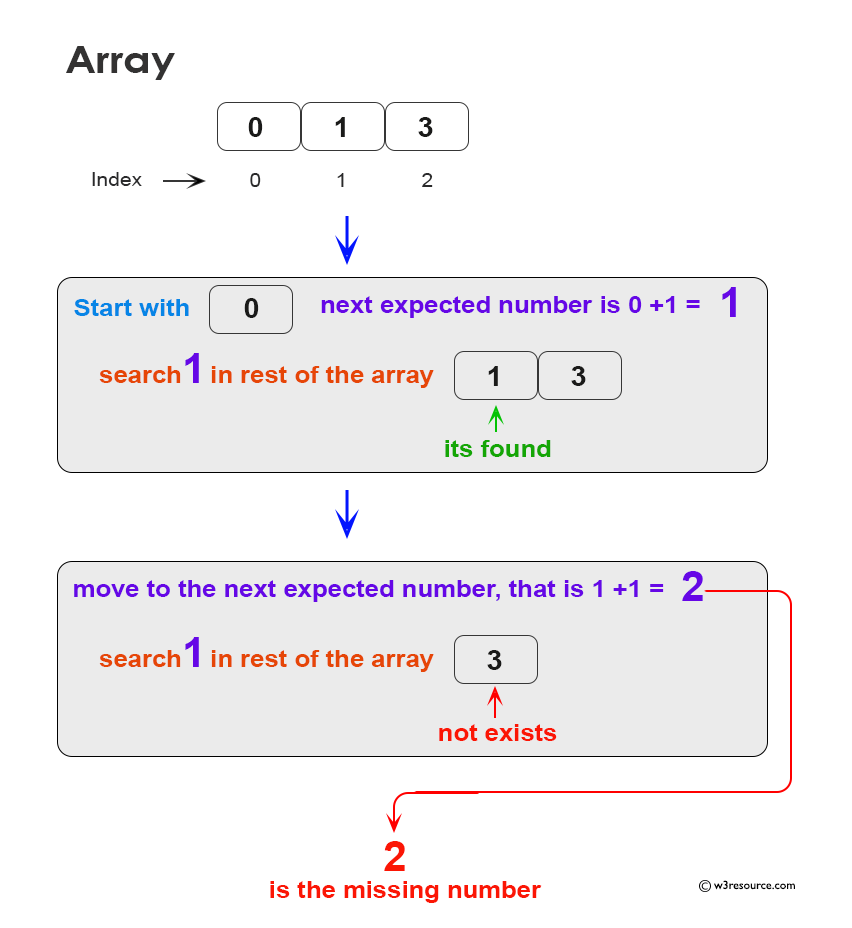
Examples and Illustrations:

Walkthrough Examples:

Example 1: Consider the array [0, 1, 3]. The missing number is 2.

Start with the first number 0.
Check if the next number exists. Here, it's 1, and it's present.
Move to the next expected number. Here, it's 2, but it's missing.
We found the missing number, which is 2.

Example 2: Take the array [4, 1, 0, 3]. The missing number is 2.

Start with the first number 4.
Check if the next number exists. Here, it's 1, and it's present.
Move to the next expected number. Here, it's 2, but it's missing.
We found the missing number, which is 2.

Visualization:

Data Structure: DSA Find the missing numbers

Brute Force Approach:

The Brute Force Approach is a straightforward and exhaustive algorithmic technique that involves checking all possible solutions to a problem. This is done to find the one that meets the criteria.

Naive Solution: The brute force approach for finding the missing number involves iterating through the array and checking each number to find the one that is missing. The steps include:

Sequential search:

Start with the number 0.
Iterate through each element in the array to check if it exists.
If a number is not found in the array, it is the missing number.

Complexity Analysis:

Time and space complexity of the brute force approach.

Time complexity:

The time complexity of this approach is O(n), where 'n' is the size of the array.
Each element in the array is checked once, leading to linear time complexity.

Space complexity:

The space complexity is O(1) since we don't use additional data structures proportional to the input size.

Efficiency:

While this approach is simple and efficient for finding the missing number, it may not be suitable for very large datasets.
It is a practical solution for small to medium-sized arrays.

Use cases:

The brute force approach is effective when the array size is not too large and optimization is not a primary concern.
It provides a baseline solution for finding the missing number but may not scale well for very large datasets or real-time applications.

Optimization Techniques:

Mathematical Approach:

Introduction:

The mathematical approach involves utilizing the properties of arithmetic progression and summation to find the missing number efficiently.

Steps:

Calculate the expected sum of the numbers from 0 to n using the formula: (n * (n + 1)) / 2.
Compute the actual sum of the given array.
The missing number is the difference between the expected sum and the actual sum.

Benefits:

This approach has a time complexity of O(n) and a space complexity of O(1), making it highly efficient.
It avoids the need for additional data structures or complex algorithms.

Use Cases:

Suitable for scenarios where memory usage needs to be minimized.
Particularly effective for large arrays with distinct numbers.

Bit Manipulation:

Introduction:

Bit manipulation techniques offer an alternative approach to finding the missing number by exploiting bitwise XOR operations.

Steps:

Initialize a variable missing to n.
Iterate through the array and perform bitwise XOR between missing and the current index ‘i’ and the array element at index ‘i’.
The result will be the missing number.

Benefits:

This approach has a time complexity of O(n) and a space complexity of O(1), making it efficient in terms of both time and space.
It is particularly useful for scenarios where bitwise operations are acceptable and can result in optimized solutions.

Use Cases:

Suitable for scenarios where bitwise manipulation is permissible and can lead to more compact and efficient solutions.
Commonly used in low-level programming and optimization tasks.

Sorting:

Introduction:

The sorting approach involves sorting the array and then iterating through it to find the missing number.

Steps:

Sort the given array in ascending order.
Iterate through the sorted array and check for any gaps between consecutive numbers.
The first occurrence of a gap indicates the missing number.

Benefits:

While this approach has a time complexity of O(n log n) due to sorting, it offers simplicity and ease of implementation.
It requires only constant additional space beyond the input array.

Use Cases:

Suitable for scenarios where the overhead of sorting is acceptable and simplicity in implementation is valued.
Applicable when the array size is not too large and efficiency is not a primary concern.

Complexity analysis:

Mathematical Approach:

Time Complexity: O(n)

Calculating the expected sum of numbers from 0 to n takes constant time.
Summing up the elements of the given array also takes linear time, as it requires traversing the entire array once.
Therefore, the overall time complexity is dominated by the linear traversal of the array.

Space Complexity: O(1)

This approach only requires a constant amount of additional space to store variables for calculations.
The space complexity is independent of the size of the input array and remains constant.
Hence, space complexity is O(1).

Bit Manipulation:

Time Complexity: O(n)

Iterating through the array to perform bitwise XOR operations takes linear time, as it requires traversing each element once.
Therefore, the time complexity is O(n).

Space Complexity: O(1)

Similar to the mathematical approach, the bit manipulation approach requires only a constant amount of additional space for storing variables.
The space complexity remains constant regardless of the size of the input array, making it O(1).

Sorting:

Time Complexity: O(n log n)

Sorting the input array using comparison-based sorting algorithms like QuickSort or MergeSort requires O(n log n) time in the average and worst-case scenarios.
After sorting, iterating through the sorted array to find the missing number takes linear time, which is dominated by the sorting operation.

Space Complexity: O(1)

Space complexity is constant because sorting is performed in-place, and no additional space is required beyond the input array.

Algorithmic Thinking:

Divide and Conquer:

Breaking Down the Problem:

Divide and Conquer breaks down a complex problem into smaller, more manageable subproblems.
For the "Find the Missing Number" problem, initially, the task might seem daunting, but by breaking it into smaller steps, it becomes more feasible.

Steps for Divide and Conquer:

Identify Key Subproblems:

Determine the missing number in the smaller subsets of the array.

Solve Each Subproblem Independently:

Calculate the missing number in each subset.

Combine the solutions:

Aggregate the missing numbers from all subsets to determine the overall missing number.

Application to "Find the Missing Number":

Identifying Subproblems:

Find the missing number within a subset of the array.
Combining the missing numbers from subsets to determine the overall missing number.

Effectiveness:

Divide and Conquer is effective for problems that can be broken down into smaller, more manageable parts.
Each subproblem is addressed independently, simplifying the overall problem-solving process.

Algorithmic Strategies:

Introduction:

Algorithmic strategies are systematic methods used to tackle problems efficiently.
In the context of finding the missing number in an array, algorithmic strategies offer approaches to optimize the solution process.

Using Arithmetic Progression:

Introduce the concept of the sum of the first n natural numbers, which forms an arithmetic progression.
Utilize the formula for the sum of an arithmetic progression to find the missing number.

Bit Manipulation:

Explore the application of bitwise XOR operation to efficiently find the missing number.
Discuss how XOR can help cancel out duplicate numbers and isolate the missing one.

Algorithmic Efficiency:

Algorithmic strategies aim to streamline problem-solving processes and reduce time complexity.
The strategies presented for finding the missing number offer alternatives to brute-force methods, optimizing efficiency.

Adaptability:

Algorithmic strategies are versatile and adaptable to various problem scenarios.
They can be applied to different problem domains by leveraging their underlying principles.

Problem-Specific Strategy:

The choice of strategy depends on the nature of the problem and its specific requirements.
Understanding the characteristics of the missing number problem guides the selection of the most suitable strategy.

Common Mistakes and Pitfalls:

Edge Cases:

Handling Empty Array:

Mistake: Assuming the array always contains elements.
Solution: Check for an empty array at the beginning and handle it appropriately to avoid errors.

Dealing with Single Element Array:

Mistake: Not considering the case where the array has only one element.
Solution: Ensure the algorithm works correctly for arrays with one or two elements.

Extreme Values:

Mistake: Ignoring edge cases with extreme values (e.g., very large or very small integers).
Solution: Test the algorithm with extreme values to verify its robustness.

Handling Duplicate Numbers:

Ignoring Duplicate Numbers:

Mistake: Overlooking the possibility of duplicate numbers in the array.
Solution: Account for duplicate numbers and decide whether to include them in the result or not.

Considering the Missing Number Twice:

Mistake: Counting the missing number twice when calculating the sum of the array.
Solution: Ensure the missing number is accounted for only once in the calculations.

Zero as an element:

Missing Zero as a Missing Number:

Mistake: Not testing the algorithm with the possibility of zero being the missing number.
Solution: Explicitly test the algorithm with scenarios where zero is the missing number to verify correctness.

Overflow and Underflow:

Ignoring Integer Overflow:

Mistake: Not considering the possibility of integer overflow when calculating sums.
Solution: Use data types that can handle large sums or implement checks to prevent overflow.

Underestimating the Data Range:

Mistake: Assuming the data range is within a certain limit.
Solution: Be mindful of the potential range of data and choose appropriate data types.

Handling negative numbers:

Misinterpreting negative numbers:

Mistake: Misinterpreting how negative numbers impact the search for the missing number.
Solution: Understand the impact of negative numbers on the search process and adjust the algorithm accordingly.

Coding Best Practices:

Modularity:

Break down the solution into modular functions or methods, each addressing a specific subtask.
Encapsulate logic related to specific functionalities within dedicated functions.
Advantages of modularity

Improved readability: Each function focuses on a specific task, making the code easier to understand.
Reusability: Modular functions can be reused in other parts of the code or in different projects.
Easy debugging: Isolate and troubleshoot issues in specific modules without affecting the entire codebase.

Example (Python code):

def find_missing_number(nums):
    # Function for finding the missing number in the array
    # ...

def main():
    # Main function to orchestrate the program
    # ...

if __name__ == "__main__":
    main()

Variable Naming:

Choose descriptive and meaningful variable names that convey the purpose or content of the variable.
Avoid single-letter variable names unless they represent common conventions (e.g., loop indices).
Benefits of good variable naming:

Readability: Clear and descriptive names enhance code readability for yourself and others.
Maintenance: Easier maintenance as the purpose of variables is evident.
Reduced comments: Well-named variables can reduce excessive comments.

Example (Python code):

def find_missing_number(nums):
    # nums: Input array of distinct numbers
    # ...
    for index, num in enumerate(nums):
        missing_num = ...

Consistency:

Maintain a consistent coding style throughout the codebase.
Follow established conventions for uniform appearance.
Version control and collaboration:

Consistency facilitates version control and collaboration, especially in team environments.
Adopting a consistent style ensures team members can easily understand and contribute to code.

Example (Python code)

# Inconsistent Style
def findMissingNumber(nums, target):
    for i, n in enumerate(nums):
        missing_num = ...
        # ...

# Consistent Style (Following PEP 8)
def find_missing_number(nums, target):
    for i, num in enumerate(nums):
        missing_num = ...
        # ...

Testing and Debugging:

Test cases:

Test Case Selection:

Test the solution with a variety of input scenarios to ensure its correctness.
Include both typical cases and edge cases to cover a wide range of possibilities.

Example Test Cases for "Find the Missing Number":

Cases with arrays containing varying numbers of elements.
Cases with different ranges of numbers (e.g., [0, 1, 2, 3] or [1, 2, 3, 4]).
Cases with missing numbers at different positions within the array.
Edge cases with empty arrays, single-element arrays, and extreme values.

Test Case Execution:

Automate the execution of test cases to streamline the testing process.
Use testing frameworks or write custom test scripts to cover various scenarios.

Debugging techniques:

Print Statements:

Insert print statements strategically to output variable values and intermediate results.
Helps identify where the code deviates from expected behavior.

Use a debugger:

Utilize integrated development environment (IDE) debuggers to set breakpoints and step through the code.
Inspect variable values and control flow to pinpoint issues.

Code Review:

Engage in code reviews with peers or mentors.
External perspectives can reveal overlooked errors or suggest alternative approaches.

Rubber Duck Debugging:

Explain the code step by step to an inanimate object (or a colleague).
The act of verbalizing often helps in identifying logical errors.

Isolated sections:

Temporarily comment out or isolate specific sections of code to identify the source of errors.
Narrow down the scope of investigation to smaller segments.

Check variable values:

Ensure that variables hold expected values at different stages of execution.
Pay attention to changes in variable states.

Use exception handling:

Implement exception handling to catch and log errors.
This prevents the program from crashing abruptly, providing information about the error.

Reproduce the issue:

Try reproducing the issue in a controlled environment.
Identify the steps leading to the error and examine the relevant code.

Logging:

Incorporate logging statements to record the program's state during execution.
Log messages provide insights into the program flow and variable values.

Test incrementally:

Implement and test the solution incrementally, focusing on small sections at a time.
Detect issues early in the development process.

Pair Programming:

Collaborate with a partner in a pair programming session.
Two sets of eyes can catch errors more effectively.

Algorithm Analysis:

Time and Space Complexity:

Time Complexity Analysis:

Evaluate the efficiency of the algorithm concerning input size.
Identify the dominant operations and quantify their relationship with input size.

Example:

For the Brute Force approach to finding the missing number, iterating through the array once results in a time complexity of O(n).
Each iteration involves constant-time operations.
Overall, the time complexity remains O(n).

Space Complexity Analysis:

Assess the algorithm's memory usage concerning input size.
Consider additional data structures and their impact on space complexity.

Example:

The Brute Force approach typically has minimal space complexity as it doesn't require additional data structures.
The space complexity remains O(1) since it only uses a few variables to store indices and values.

Trade-offs:

Time vs. Space Complexity:

Evaluate the trade-offs between optimizing for time or space.
Some algorithms prioritize reduced time complexity, while others prioritize minimal space usage.

Example Trade-off:

The Brute Force approach has optimal space complexity but may not be the most efficient for large datasets due to its linear time complexity.

Memory Efficiency vs. Speed:

Consider the balance between memory efficiency and algorithmic speed.
Optimize the algorithm based on the specific requirements and constraints of the problem.

Example Trade-off:

The Brute Force approach sacrifices time efficiency for minimal memory usage, making it suitable for scenarios where memory constraints are critical.

Algorithmic Strategies:

Choose algorithmic strategies based on the problem's characteristics and constraints.
Select an approach that aligns with the specific goals of the application.

Example Trade-off:

While the Brute Force approach is straightforward and easy to implement, it may not be the most efficient for large datasets. In such cases, alternative strategies like bitwise operations or mathematical formulas may offer better performance.

Scalability:

Consider how well the algorithm scales as the input size increases.
Choose an algorithm that maintains efficiency with growing datasets.

Example Trade-off:

The Brute Force approach scales linearly with the input size, making it suitable for small to moderate datasets but inefficient for very large arrays. In such cases, more scalable algorithms like binary search or bitwise operations may be preferable.

Application in Real-world Projects:

Practical Use Cases:

Inventory Management Systems:

Scenario: In inventory management, tracking missing items or identifying discrepancies in stock levels is crucial.
Algorithmic Approach: The missing number problem can be applied to efficiently identify the absence of specific items in the inventory.

Error Detection in Data Transmission:

Scenario: During data transmission over networks, errors can occur, resulting in missing or corrupted data packets.
Algorithmic Approach: By leveraging the missing number problem, systems can detect missing or corrupted packets by analyzing the sequence of received data.

Healthcare Records Management:

Scenario: Ensuring completeness and accuracy in healthcare records is essential for patient care and medical research.
Algorithmic Approach: The missing number problem can assist in identifying missing patient records or anomalies in medical datasets, enhancing data integrity.

Examining Census Data:

Scenario: Analyzing census data for demographic studies or resource allocation requires accurate population counts.
Algorithmic Approach: Utilizing the missing number problem, discrepancies or missing data points in census records can be identified, improving the reliability of demographic analyses.

Digital Forensics:

Scenario: In digital forensics investigations, reconstructing timelines or sequences of events from fragmented data is a common challenge.
Algorithmic Approach: The missing number problem can aid in reconstructing missing or tampered data sequences, assisting forensic analysts in piecing together digital evidence.

Further Exploration:

Exploring Additional Challenges:

Variations of the missing number problem can include scenarios with duplicate numbers, shuffled sequences, or multiple missing numbers within the array.
Challenge learners to adapt the solution to handle irregularities in input data or different numbering schemes.

Example test cases:

Positive cases with valid missing numbers:

Input: nums = [0, 1, 3], Expected output: 2 (as the missing number is 2)
Input: nums = [9, 6, 4, 2, 3, 5, 7, 0, 1], Expected output: 8 (as the missing number is 8)

Negative cases with no missing numbers:

Input: nums = [0, 1, 2, 3], Expected output: None (no missing number)
Input: nums = [5, 4, 3, 2, 1, 0], Expected output: None (no missing number)

Edge cases with empty arrays, single-element arrays, and extreme values:

Input: nums = [], Expected output: None (empty array)
Input: nums = [0], Expected output: None (single-element array)
Input: nums = [1000000000, 999999999, 999999998, ..., 3, 2, 1], Expected output: 0 (as the missing number is 0)

Solution for different languages:

Python - Find the Missing Number

Code:

# Python Solution

def find_missing_number(nums):
    # Calculate the expected sum of numbers from 0 to n
    expected_sum = len(nums) * (len(nums) + 1) // 2
    
    # Calculate the actual sum of the numbers in the array
    actual_sum = sum(nums)
    
    # The missing number is the difference between the expected sum and the actual sum
    missing_number = expected_sum - actual_sum
    
    return missing_number

# Test Cases
test_cases = [
    ([3, 0, 1]),       
    ([9, 6, 4, 2, 3, 5, 7, 0, 1]),
    ([1, 2, 3, 4]),
    ([])                 
]

for nums in test_cases:
    result = find_missing_number(nums)
    print(f"Input: {nums}, Missing Number: {result}")

Output:

Input: [3, 0, 1], Missing Number: 2
Input: [9, 6, 4, 2, 3, 5, 7, 0, 1], Missing Number: 8
Input: [1, 2, 3, 4], Missing Number: 0
Input: [], Missing Number: 0

Explanation of the said Python code:

expected_sum = len(nums) (len(nums) + 1) // 2: This line calculates the expected sum of numbers from 0 to n using the formula for the sum of an arithmetic series: n (n + 1) / 2. Here, 'len(nums)' represents 'n'.
actual_sum = sum(nums): This line calculates the actual sum of the numbers in the input list 'nums' using the "sum()" function.
missing_number = expected_sum - actual_sum: This line calculates the missing number by subtracting the actual sum from the expected sum. The missing number will be the difference between the sum of the sequence from 0 to 'n' and the sum of the numbers in the list 'nums'.
Finally, the function returns the 'missing_number'.

Java - Find the Missing Numbers Solution

Code:

// Java Solution
import java.util.Arrays;
public class FindMissingNumber {
    public static int findMissingNumber(int[] nums) {
        // Calculate the expected sum of numbers from 0 to n
        int n = nums.length;
        int expectedSum = n * (n + 1) / 2;
        
        // Calculate the actual sum of the numbers in the array
        int actualSum = 0;
        for (int num : nums) {
            actualSum += num;
        }
        
        // The missing number is the difference between the expected sum and the actual sum
        int missingNumber = expectedSum - actualSum;
        
        return missingNumber;
    }
    
    public static void main(String[] args) {
        // Test Cases
        int[][] testCases = {
            {3, 0, 1},         
            {9, 6, 4, 2, 3, 5, 7, 0, 1}, 
            {1,2,3,4},
            {}      
        };
        
        for (int[] nums : testCases) {
            int result = findMissingNumber(nums);
            // Print the array elements
            System.out.println("Input: " + Arrays.toString(nums) + ", Missing Number: " + result);
             
   
        }
    }
}

Output:

Input: [3, 0, 1], Missing Number: 2
Input: [9, 6, 4, 2, 3, 5, 7, 0, 1], Missing Number: 8
Input: [1, 2, 3, 4], Missing Number: 0
Input: [], Missing Number: 0

Explanation of the said Java code:

findMissingNumber(int[] nums): This method takes an array of integers 'nums' as input and returns the missing number in the sequence from 0 to 'n', where 'n' is the length of the array 'nums'.

It calculates the expected sum of numbers from 0 to 'n' using the formula n * (n + 1) / 2.
It calculates the actual sum of the numbers in the input array 'nums' by iterating through the array and adding each element to the 'actualSum' variable.
It calculates the missing number by subtracting the actual sum from the expected sum.
Finally, it returns the 'missingNumber'.

main(String[] args): This method serves as the entry point of the program. It contains test cases to demonstrate the functionality of the "findMissingNumber()" method.

C++ - Find the Missing Numbers Solution

Code:

// C++ Solution
#include <iostream>
#include <vector>


using namespace std;

int findMissingNumber(vector<int>& nums) {
    // Calculate the expected sum of numbers from 0 to n
    int n = nums.size();
    int expectedSum = n * (n + 1) / 2;
    
    // Calculate the actual sum of the numbers in the array
    int actualSum = 0;
    for (int num : nums) {
        actualSum += num;
    }
    
    // The missing number is the difference between the expected sum and the actual sum
    int missingNumber = expectedSum - actualSum;
    
    return missingNumber;
}

int main() {
    // Test Cases
    vector<vector<int>> testCases = {
        {3, 0, 1},       
        {9, 6, 4, 2, 3, 5, 7, 0, 1}, 
		{1,2,3,4},
	    {}                     
    };
    
    for (vector<int>& nums : testCases) {
        int result = findMissingNumber(nums);
        cout << "Input: [";
        for (int i = 0; i < nums.size(); ++i) {
            cout << nums[i];
            if (i != nums.size() - 1) {
                cout << ", ";
            }
        }
        cout << "], Missing Number: " << result << endl;
    }
    
    return 0;
}

Output:

Input: [3, 0, 1], Missing Number: 2
Input: [9, 6, 4, 2, 3, 5, 7, 0, 1], Missing Number: 8
Input: [1, 2, 3, 4], Missing Number: 0
Input: [], Missing Number: 0

Explanation of the said C++ code:

findMissingNumber(int[] nums): This method takes an array of integers 'nums' as input and returns the missing number in the sequence from 0 to 'n', where 'n' is the length of the array 'nums'.

It calculates the expected sum of numbers from 0 to 'n' using the formula n * (n + 1) / 2.
It calculates the actual sum of the numbers in the input array 'nums' by iterating through the array and adding each element to the 'actualSum' variable.
It calculates the missing number by subtracting the actual sum from the expected sum.
Finally, it returns the 'missingNumber'.

main(String[] args): This method serves as the entry point of the program. It contains test cases to demonstrate the functionality of the "findMissingNumber()" method.

C# - Find the Missing Numbers Solution

Code:

// C# Solution

using System;
using System.Collections.Generic;

class Program
{
    static int FindMissingNumber(int[] nums)
    {
        // Calculate the expected sum of numbers from 0 to n
        int n = nums.Length;
        int expectedSum = n * (n + 1) / 2;

        // Calculate the actual sum of the numbers in the array
        int actualSum = 0;
        foreach (int num in nums)
        {
            actualSum += num;
        }

        // The missing number is the difference between the expected sum and the actual sum
        int missingNumber = expectedSum - actualSum;

        return missingNumber;
    }

    static void Main(string[] args)
    {
        // Test Cases
        int[][] testCases = new int[][]
        {
            new int[] {3, 0, 1},
            new int[] {9, 6, 4, 2, 3, 5, 7, 0, 1},
            new int[] {1, 2, 3, 4 },
            new int[] {}
        };
        foreach (int[] nums in testCases)
        {
            int result = FindMissingNumber(nums);
            Console.WriteLine($"Input: [{string.Join(", ", nums)}], Missing Number: {result}");
        }
    }
}

Output:

Input: [3, 0, 1], Missing Number: 2
Input: [9, 6, 4, 2, 3, 5, 7, 0, 1], Missing Number: 8
Input: [1, 2, 3, 4], Missing Number: 0
Input: [], Missing Number: 0

Explanation of the said C# code:

FindMissingNumber method:

This method takes an integer array 'nums' as input and returns an integer representing the missing number in the sequence from 0 to n, where 'n' is the length of the array.
It calculates the expected sum of numbers from 0 to n using the formula n * (n + 1) / 2.
It calculates the actual sum of the numbers in the input array 'nums' by iterating through the array and adding each element to the 'actualSum' variable.
It calculates the missing number by subtracting the actual sum from the expected sum.
Finally, it returns the 'missingNumber'.

Main method:
- This method serves as the entry point of the program.
- It defines an array of test cases, where each test case is represented by an integer array.

JavaScript - Find the Missing Number Solution

Code:

// JavaScript Solution

function findMissingNumber(nums) {
    // Calculate the expected sum of numbers from 0 to n
    const n = nums.length;
    const expectedSum = (n * (n + 1)) / 2;
    
    // Calculate the actual sum of the numbers in the array
    let actualSum = 0;
    for (const num of nums) {
        actualSum += num;
    }
    
    // The missing number is the difference between the expected sum and the actual sum
    const missingNumber = expectedSum - actualSum;
    
    return missingNumber;
}

// Test Cases
const testCases = [
    [3, 0, 1],           
    [9, 6, 4, 2, 3, 5, 7, 0, 1],  
    [1, 2, 3, 4],
    []                    
];

testCases.forEach(nums => {
    const result = findMissingNumber(nums);
    console.log(`Input: [${nums}], Missing Number: ${result}`);
});

Output:

"Input: [3,0,1], Missing Number: 2"
"Input: [9,6,4,2,3,5,7,0,1], Missing Number: 8"
"Input: [1,2,3,4], Missing Number: 0"
"Input: [], Missing Number: 0"

Explanation of the said JavaScript code

findMissingNumber function:

This function takes an array 'nums' as input and returns the missing number in the sequence from 0 to n, where 'n' is the length of the array.
It calculates the expected sum of numbers from 0 to n using the formula (n * (n + 1)) / 2.
It calculates the actual sum of the numbers in the input array 'nums' by iterating through the array and adding each element to the 'actualSum' variable.
It calculates the missing number by subtracting the actual sum from the expected sum.
Finally, it returns the 'missingNumber'

Time and Space Complexity:

Time Complexity:

Calculating the expected sum of numbers from 0 to n takes constant time, represented as O(1).
Calculating the actual sum of the numbers in the array using the "sum()" function has a time complexity of O(n), where 'n' is the length of the input array 'nums'.
Finding the missing number by subtracting the actual sum from the expected sum takes constant time, represented as O(1).

Space complexity:

The algorithm uses only a constant amount of additional space, regardless of the size of the input array 'nums'.
It does not create any additional data structures that grow with the input size.
Therefore, the space complexity is O(1), indicating a constant space complexity.