Java: Find the longest increasing continuous subsequence in a given array of integers

Last update on May 13 2025 13:00:29 (UTC/GMT +8 hours)

Longest Increasing Subsequence

Write a Java program to find the longest increasing continuous subsequence in a given array of integers.

Visual Presentation:

Sample Solution:

Java Code:

// Importing necessary Java utilities
import java.util.*;

// Main class Solution
public class Solution {
    // Main method
    public static void main(String[] args) {
        // Initializing an array of integers
        int[] nums = { 10, 11, 12, 13, 14, 7, 8, 9, 1, 2, 3 };
        
        // Printing the original array
        System.out.println("Original array: " + Arrays.toString(nums));
        
        // Finding the size of the longest increasing continuous subsequence and printing it
        System.out.println("Size of longest increasing continuous subsequence: " + longest_seq(nums));
    }

    // Method to find the size of the longest increasing continuous subsequence
    public static int longest_seq(int[] nums) {
        int max_sequ = 0; // Initializing the variable to hold the maximum sequence length
        
        // Handling the case when the array contains only one element
        if (nums.length == 1) 
            return 1; // If only one element is present, the longest sequence is of length 1

        // Looping through the array to find the longest increasing or decreasing sequence
        for (int i = 0; i < nums.length - 1; i++) {
            int ctr = 1; // Counter to track the sequence length
            int j = i; // Initializing j to the current index i
            
            // Checking for an increasing sequence
            if (nums[i + 1] > nums[i]) {
                while (j < nums.length - 1 && nums[j + 1] > nums[j]) {
                    ctr++; // Incrementing the counter for each increasing element
                    j++;
                }
            } 
            // Checking for a decreasing sequence
            else if (nums[i + 1] < nums[i]) {
                while (j < nums.length - 1 && nums[j + 1] < nums[j]) {
                    ctr++; // Incrementing the counter for each decreasing element
                    j++;
                }
            }
            
            // Updating the maximum sequence length encountered so far
            if (ctr > max_sequ) {
                max_sequ = ctr;
            }
            
            // Moving the index i ahead by the sequence length minus 2 to avoid rechecking elements
            i += ctr - 2;
        }
        
        return max_sequ; // Returning the size of the longest sequence found
    }
} 

Sample Output:

Original array: [10, 11, 12, 13, 14, 7, 8, 9, 1, 2, 3]
Size of longest increasing continuous subsequence: 5

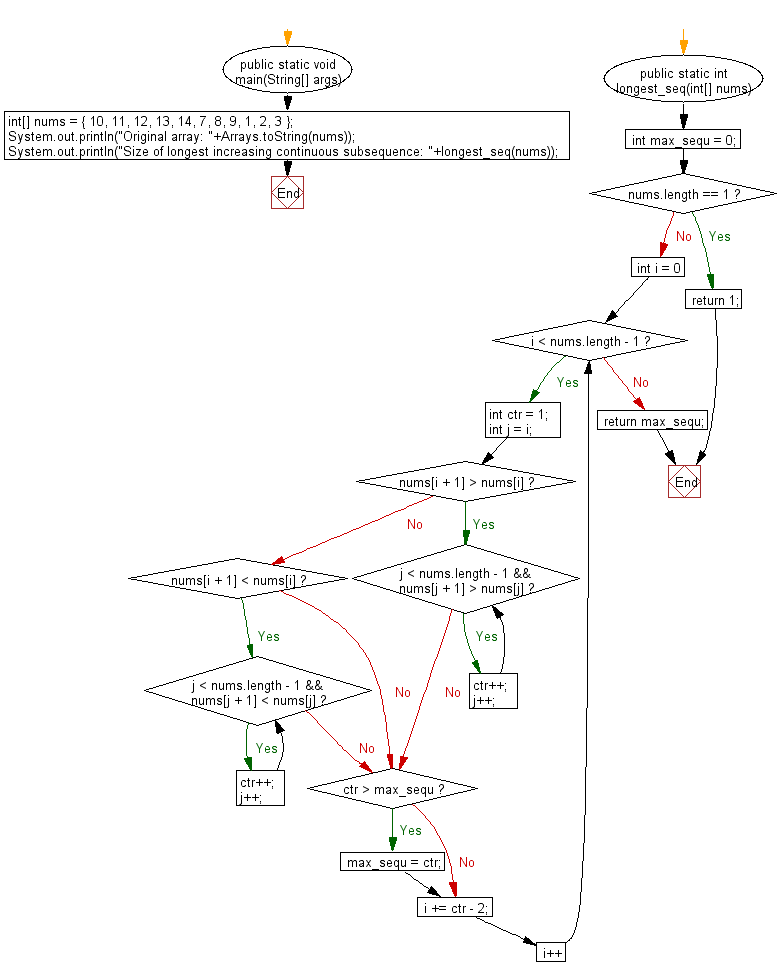
Flowchart:

For more Practice: Solve these Related Problems:

• Write a Java program to find the longest increasing subsequence (not necessarily continuous) in an array.
• Write a Java program to determine the longest decreasing continuous subsequence in an array of integers.
• Write a Java program to find the longest subsequence in which elements alternate between increasing and decreasing.
• Write a Java program to compute the longest increasing continuous subsequence in an array that includes duplicate values.

Go to:

• Java Basic Part-II Programming Exercises Home ↩
• Java Exercises Home ↩

PREV : Clone Binary Tree.
NEXT : Add One to Array Number.

Java Code Editor:

Company:  Facebook

Contribute your code and comments through Disqus.