Java: Reads n digits (given) chosen from 0 to 9 and prints the number of combinations

Last update on May 13 2025 12:58:55 (UTC/GMT +8 hours)

Count Combinations of Digits with Target Sum

Write a Java program that reads n digits (given) chosen from 0 to 9 and prints the number of combinations where the sum of the digits equals another given number (s). Do not use the same digits in a combination.

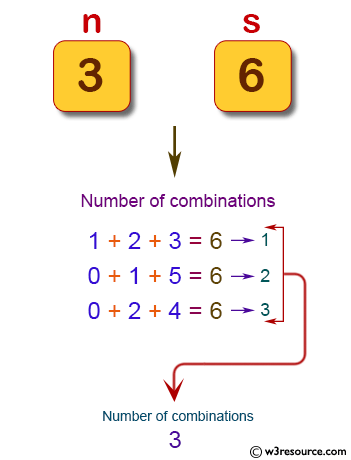
For example, the combinations where n = 3 and s = 6 are as follows:
1 + 2 + 3 = 6
0 + 1 + 5 = 6
0 + 2 + 4 = 6

Input:

Two integers as number of combinations and their sum by a single space in a line. Input 0 0 to exit.

Visual Presentation:

Sample Solution:

Java Code:

// Importing the Scanner class for user input
import java.util.*;

// Main class named "Main"
public class Main {
    
    // Main method to execute the program
    public static void main(String[] args) {
        // Creating a Scanner object for user input
        Scanner stdIn = new Scanner(System.in);

        // Prompting the user to input the number of combinations and sum (separated by a space in a line)
        System.out.println("Input number of combinations and sum (separated by a space in a line):");

        // Reading the number of combinations (n) and the sum (s) from the user
        int n = stdIn.nextInt();
        int s = stdIn.nextInt();

        // Calling the comnum method to calculate the number of combinations
        int c1 = comnum(0, n, s, 0);

        // Prompting the user with the number of combinations
        System.out.println("Number of combinations:");
        System.out.println(c1);
    }

    // Recursive method to calculate the number of combinations
    public static int comnum(int i, int n, int s, int p) {
        // Base case: If the sum (p) matches the target sum (s) and no more elements (n) are left
        if (s == p && n == 0) {
            return 1;
        }

        // Base case: If all elements are considered (i reaches 10), return 0
        if (i >= 10) {
            return 0;
        }

        // Base case: If the sum (p) exceeds the target sum (s), return 0
        if (p > s) {
            return 0;
        }

        // Recursive calls for including and excluding the current element
        int c1 = comnum(i + 1, n - 1, s, p + i);
        int c2 = comnum(i + 1, n, s, p);

        // Returning the sum of combinations from both recursive calls
        return c1 + c2;
    }
} 

Sample Output:

Input number of combinations and sum (separated by a space in a line):
3 6
Number of combinations:
3

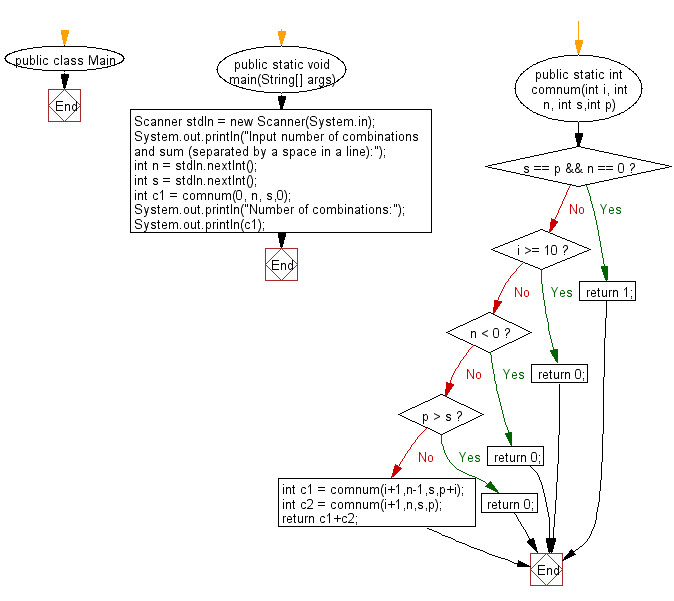
Flowchart:

For more Practice: Solve these Related Problems:

• Write a Java program to count unique combinations of n digits (0–9) that sum to a target without repeating any digit.
• Write a Java program to count combinations of digits that sum to a target using recursion with memoization.
• Write a Java program to determine the number of digit combinations summing to a target and output one valid combination.
• Write a Java program to compute the number of combinations of digits that sum to a target, ensuring the digits appear in increasing order.

Go to:

• Java Basic Part-II Programming Exercises Home ↩
• Java Exercises Home ↩

PREV : Most Frequent and Longest Words in Text.
NEXT : Check Rectangle or Rhombus from Parallelogram Sides.

Java Code Editor:

Contribute your code and comments through Disqus.