Java: Find a specified element in a given sorted array of elements using Exponential search

Java Search: Exercise-5 with Solution

Write a Java program to find a specified element in a given sorted array of elements using Exponential search.

From Wikipedia, in computer science, an exponential search (also called doubling search or galloping search or Struzik search) is an algorithm, created by Jon Bentley and Andrew Chi-Chih Yao in 1976, for searching sorted, unbounded/infinite lists. There are numerous ways to implement this with the most common being to determine a range that the search key resides in and performing a binary search within that range. This takes O(log i) where i is the position of the search key in the list, if the search key is in the list, or the position where the search key should be, if the search key is not in the list.

Sample Solution:

Java Code:

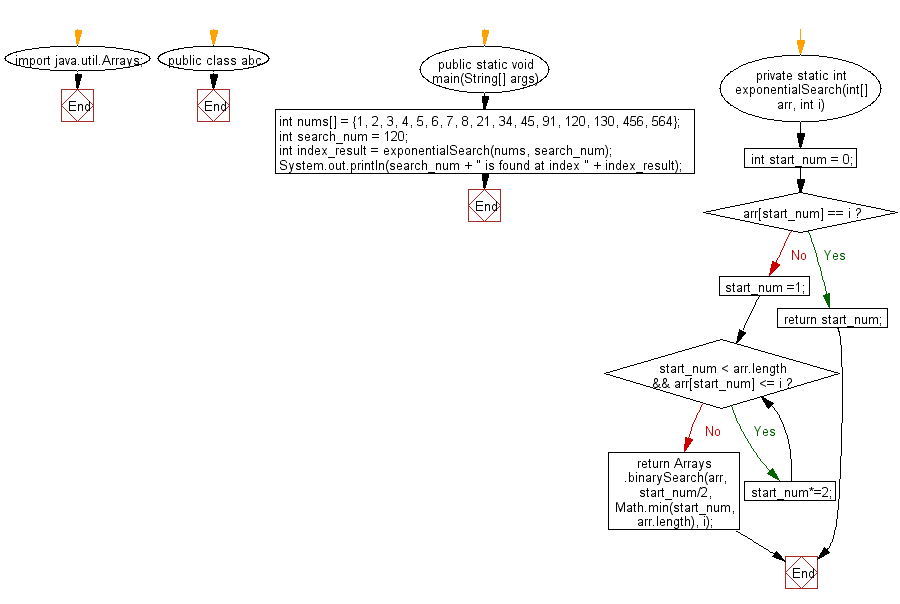
import java.util.Arrays;
public class abc {
	public static void main(String[] args) {
		int nums[] = {1, 2, 3, 4, 5, 6, 7, 8, 21, 34, 45, 91, 120, 130, 456, 564};
        int search_num = 120;
		
		// Find the index of searched item
       int index_result = exponentialSearch(nums, search_num);

       System.out.println(search_num + " is found at index " + index_result);		
		
	}

	private static int exponentialSearch(int[] arr, int i) {
		int start_num = 0;
		
		if(arr[start_num] == i)
			return start_num;
		start_num =1;
		while(start_num < arr.length && arr[start_num] <= i) {
			start_num*=2;
		}
		return Arrays.binarySearch(arr, start_num/2, Math.min(start_num, arr.length), i);
	}
}

Sample Output:

120 is found at index 12

Flowchart:

Java Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Java program to find a specified element in a given array of elements using Interpolation Search.
Next: Write a Java program to find a specified element in a given array of elements using Ternary search.