JavaScript: Calculate Lanczos approximation gamma

JavaScript Math: Exercise-49 with Solution

Lanczos Approximation Gamma Function

Write a JavaScript function to calculate the Lanczos approximation gamma.

In mathematics, the Lanczos approximation is a method for computing the Gamma function numerically, published by Cornelius Lanczos in 1964. It is a practical alternative to the more popular Stirling's approximation for calculating the Gamma function with fixed precision.

Sample Solution:

JavaScript Code:

// Define a function named Lanczos_Gamma that calculates the Lanczos approximation of the gamma function for the given input 'num'.
function Lanczos_Gamma(num) 
{
  // Define the coefficients of the Lanczos approximation.
  var p = [
    0.99999999999980993, 676.5203681218851, -1259.1392167224028,
    771.32342877765313, -176.61502916214059, 12.507343278686905, -0.13857109526572012, 9.9843695780195716e-6, 1.5056327351493116e-7
  ];
  var i;
  var g = 7;
  
  // Check if the input is less than 0.5 and return the reciprocal identity if true.
  if (num < 0.5) return Math.PI / (Math.sin(Math.PI * num) * calculus.LanczosGamma(1 - num));
  
  // Adjust the input value.
  num -= 1;
  
  // Initialize 'a' and 't'.
  var a = p[0];
  var t = num + g + 0.5;
  
  // Calculate the Lanczos approximation using the coefficients.
  for (i = 1; i < p.length; i++) {
    a += p[i] / (num + i);
  }
  
  // Return the result of the Lanczos approximation.
  return Math.sqrt(2 * Math.PI) * Math.pow(t, num + 0.5) * Math.exp(-t) * a;
}

// Output the result of Lanczos_Gamma function with input 5.
console.log(Lanczos_Gamma(5));

Output:

23.999999999999996

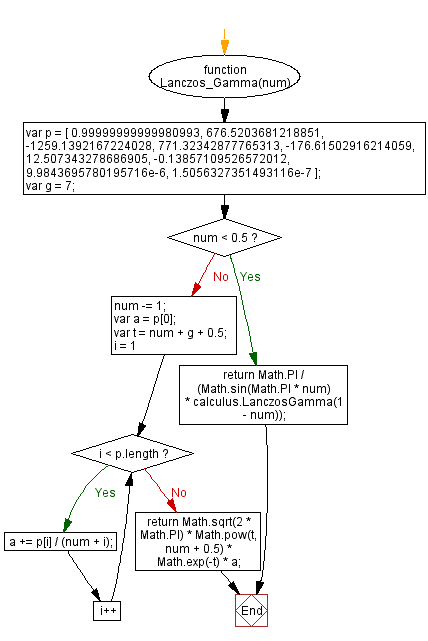
Flowchart:

Live Demo:

See the Pen javascript-math-exercise-49 by w3resource (@w3resource) on CodePen.

For more Practice: Solve these Related Problems:

• Write a JavaScript function that computes the Gamma function using the Lanczos approximation and returns a numeric value.
• Write a JavaScript function that implements the Lanczos approximation and compares its result with known Gamma values.
• Write a JavaScript function that approximates the Gamma function using Lanczos coefficients and validates precision against benchmarks.
• Write a JavaScript function that handles edge cases in the Gamma function computation, especially for non-positive inputs.

Improve this sample solution and post your code through Disqus.

Previous: Write a JavaScript function to calculate the falling factorial of a number.
Next: Write a JavaScript program to add two complex numbers.