Python: Least Common Multiple (LCM) of more than two numbers

Last update on April 17 2025 13:00:49 (UTC/GMT +8 hours)

LCM of Multiple Numbers

Write a Python program that calculates the Least Common Multiple (LCM) of more than two numbers. The numbers should be taken from a given list of positive integers.

From Wikipedia,
In arithmetic and number theory, the least common multiple, lowest common multiple, or smallest common multiple of two integers a and b, usually denoted by lcm(a, b), is the smallest positive integer that is divisible by both a and b. Since division of integers by zero is undefined, this definition has meaning only if a and b are both different from zero. However, some authors define lcm(a,0) as 0 for all a, which is the result of taking the lcm to be the least upper bound in the lattice of divisibility.

Sample Solution-1:

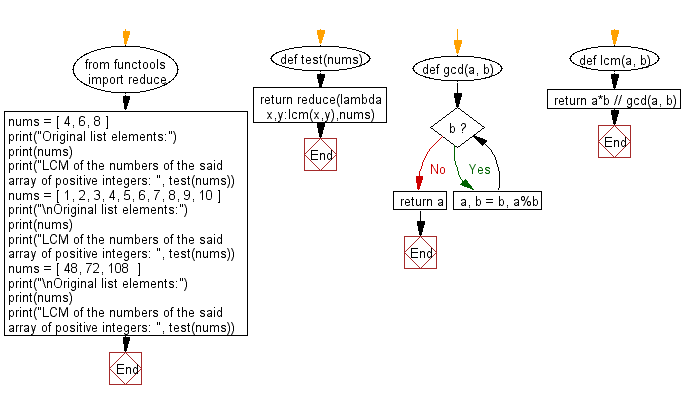
Python Code:

# Import the 'reduce' function from the 'functools' module.
from functools import reduce

# Define a function 'test' that calculates the LCM (Least Common Multiple) of a list of numbers.
def test(nums):
    # Use the 'reduce' function to apply the 'lcm' function cumulatively to the elements of 'nums'.
    return reduce(lambda x, y: lcm(x, y), nums)

# Define a function 'gcd' that calculates the Greatest Common Divisor (GCD) of two numbers.
def gcd(a, b):
    # Use the Euclidean algorithm to find the GCD of 'a' and 'b'.
    while b:
        a, b = b, a % b
    return a

# Define a function 'lcm' that calculates the Least Common Multiple (LCM) of two numbers.
def lcm(a, b):
    # Calculate the LCM using the formula: LCM(a, b) = (a * b) / GCD(a, b).
    return a * b // gcd(a, b)

# Test cases with different lists of positive integers.
nums = [4, 6, 8]
print("Original list elements:")
print(nums)
print("LCM of the numbers of the said array of positive integers: ", test(nums))

nums = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
print("\nOriginal list elements:")
print(nums)
print("LCM of the numbers of the said array of positive integers: ", test(nums))

nums = [48, 72, 108]
print("\nOriginal list elements:")
print(nums)
print("LCM of the numbers of the said array of positive integers: ", test(nums))

Sample Output:

Original list elements:
[4, 6, 8]
LCM of the numbers of the said array of positive integers:  24

Original list elements:
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
LCM of the numbers of the said array of positive integers:  2520

Original list elements:
[48, 72, 108]
LCM of the numbers of the said array of positive integers:  432

Explanation:

Here is a breakdown of the above Python code:

LCM Function (test function):

The test function takes a list of positive integers as input and calculates the LCM of the numbers.
It uses the "reduce()" function to apply the "lcm()" function cumulatively to the elements of the input list.

GCD and LCM Functions (gcd and lcm functions):

The "gcd()" function calculates the Greatest Common Divisor (GCD) of two numbers using the Euclidean algorithm.
The "lcm()" function calculates the Least Common Multiple (LCM) of two numbers using the formula: LCM(a, b) = (a * b) / GCD(a, b).

Flowchart:

Sample Solution-2:

Use functools.reduce(), math.gcd() and lcm(x,y) = x * y / gcd(x,y) over the given list.

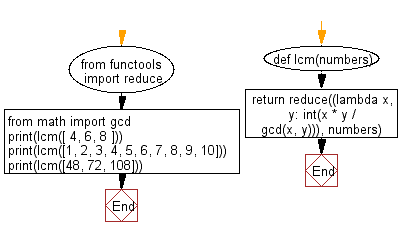
Python Code:

# Import the 'reduce' function from the 'functools' module.
from functools import reduce
# Import the 'gcd' function from the 'math' module.
from math import gcd

# Define a function 'lcm' that calculates the Least Common Multiple (LCM) of a list of numbers.
def lcm(numbers):
    # Use the 'reduce' function to apply the lambda function cumulatively to the elements of 'numbers'.
    # The lambda function calculates the LCM using the formula: LCM(a, b) = (a * b) / GCD(a, b).
    return reduce((lambda x, y: int(x * y / gcd(x, y))), numbers)

# Test cases with different lists of positive integers.
print(lcm([4, 6, 8]))
print(lcm([1, 2, 3, 4, 5, 6, 7, 8, 9, 10]))
print(lcm([48, 72, 108]))

Sample Output:

24
2520
432

Explanation:

Here is a breakdown of the above Python code:

LCM Function (lcm function):

The "lcm()" function takes a list of numbers as input and calculates the LCM of the numbers.
It uses the "reduce()" function to apply the lambda function cumulatively to the elements of the input list.
The lambda function calculates the LCM using the formula: LCM(a, b) = (a * b) / GCD(a, b).

Flowchart:

For more Practice: Solve these Related Problems:

Write a Python program to compute the least common multiple (LCM) of a list of positive integers using the gcd function.
Write a Python program to calculate the LCM of multiple numbers by iteratively applying the LCM formula pairwise.
Write a Python program to find the LCM of an array of integers using the reduce function and math.gcd.
Write a Python program to determine the smallest common multiple for a list of numbers using a pairwise LCM approach.

Go to:

Previous: Write a Python program to alternate the case of each letter in a given string and the first letter of the said string must be uppercase.
Next: Write a Python program to reverse all the words which have odd length.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.