Python: Print the length of the series and the series from the given 3rd term, 3rd last term and the sum of a series

Last update on April 17 2025 13:01:38 (UTC/GMT +8 hours)

Series Length and Terms

Write a Python program to print the length of the series and the series from the given 3rd term, 3rd last term and the sum of a series.

Let X and Y denote the third and the third last term of the arithmetic progression respectively
i.e. X=a+2d and Y=a+(n−3)d where a, d and n are what you would expect them to be.
 Note that we are given X and Y

Now, we are also given the sum of the n terms i.e. S=n2[2a+(n−1)d]

⇒S=n2[(a+2d)+(a+(n−3)d)]

⇒S=n2[X+Y]

⇒n=2SX+Y

Having computed n, we can plug back it's value in the expression for Y. 
This will give us 2 equations in 2 unknowns (a and d) which we can solve to determine the remaining variables.

X=a+2d and Y=a+(2SX+Y−3)d
Reference: https://bit.ly/2N2VM9f

Sample Data:
Input third term of the series: 3
Input 3rd last term: 3
Input Sum of the series: 15
Length of the series: 5
Series:
1 2 3 4 5

Sample Solution:

Python Code:

# Input the third term of the series
tn = int(input("Input third term of the series:"))
# Input the 3rd last term
tltn = int(input("Input 3rd last term:"))
# Input the sum of the series
s_sum = int(input("Sum of the series:"))
# Calculate the length of the series using the formula for the sum of an arithmetic series
n = int(2 * s_sum / (tn + tltn))
print("Length of the series: ", n)

# Calculate the common difference 'd' based on the length of the series
if n - 5 == 0:
    d = (s_sum - 3 * tn) // 6
else:
    d = (tltn - tn) / (n - 5)

# Calculate the first term 'a' using the third term and common difference
a = tn - 2 * d
j = 0

# Print the series
print("Series:")
for j in range(n - 1):
    print(int(a), end=" ")
    a += d
print(int(a), end=" ")

Sample Output:

Input third term of the series: 3
Input 3rd last term: 6
Sum of the series: 36
Length of the series:  8
Series:
1 2 3 4 5 6 7 8

More Sample Output:

Input third term of the series: 3
Input 3rd last term: 3
Sum of the series: 15
Length of the series:  5
Series:
1 2 3 4 5

Explanation:

Here is the breakdown of the above Python exercise:

User Input:

tn = int(input("Input third term of the series:")): Takes user input for the third term of the arithmetic series.
tltn = int(input("Input 3rd last term:")): Takes user input for the third-last term of the arithmetic series.
s_sum = int(input("Sum of the series:")): Takes user input for the sum of the arithmetic series.

Calculate Series Length:

n = int(2 * s_sum / (tn + tltn)): Calculates the length of the arithmetic series using the sum formula.

Calculate Common Difference:

Determines the common difference 'd' based on the length of the series.

If n - 5 == 0, it sets d = (s_sum - 3 * tn) // 6.
Otherwise, it sets d = (tltn - tn) / (n - 5).

Calculate First Term:

a = tn - 2 * d: Calculates the first term 'a' of the arithmetic series using the third term and common difference.

Print Series:

Prints the arithmetic series using a loop and the calculated first term and common difference.

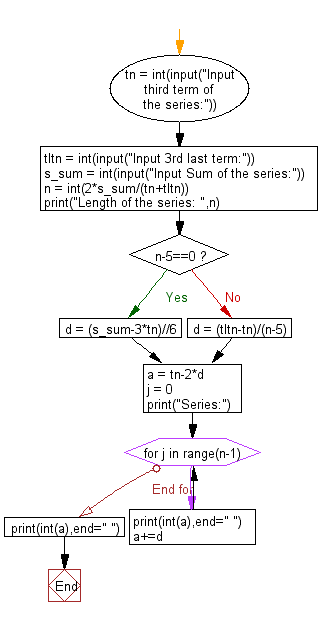
Flowchart:

For more Practice: Solve these Related Problems:

Write a Python program to compute the mean and median of a series given its first and last terms along with the total sum.
Write a Python program to verify if a series is arithmetic given its second term, second last term, and total sum.
Write a Python program to calculate the common difference of an arithmetic series based on partial series information.
Write a Python program to reconstruct an arithmetic series when given the sum, number of terms, and one specific term.

Go to:

Previous: Write a Python program to find the type of the progression (arithmetic progression/geometric progression) and the next successive member of a given three successive members of a sequence.
Next: Write a Python program to find common divisors between two numbers in a given pair.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.