Python: Sort unsorted numbers using Merge-insertion sort
39. Merge-Insertion Sort
Write a Python program to sort unsorted numbers using Merge-insertion sort.
From Wikipedia,
In computer science, merge-insertion sort or the Ford–Johnson algorithm is a comparison sorting algorithm published in 1959 by L. R. Ford Jr. and Selmer M. Johnson.It uses fewer comparisons in the worst case than the best previously known algorithms, binary insertion sort and merge sort, and for 20 years it was the sorting algorithm with the fewest known comparisons. Although not of practical significance, it remains of theoretical interest in connection with the problem of sorting with a minimum number of comparisons. The same algorithm may have also been independently discovered by Stanisław Trybuła and Czen Ping.
Sample Solution:
Python Code:
#Ref.https://bit.ly/3r32ezJ
from __future__ import annotations
def merge_insertion_sort(collection: list[int]) -> list[int]:
"""Pure implementation of merge-insertion sort algorithm in Python
:param collection: some mutable ordered collection with heterogeneous
comparable items inside
:return: the same collection ordered by ascending
Examples:
>>> merge_insertion_sort([0, 5, 3, 2, 2])
[0, 2, 2, 3, 5]
>>> merge_insertion_sort([99])
[99]
>>> merge_insertion_sort([-2, -5, -45])
[-45, -5, -2]
"""
def binary_search_insertion(sorted_list, item):
left = 0
right = len(sorted_list) - 1
while left <= right:
middle = (left + right) // 2
if left == right:
if sorted_list[middle] < item:
left = middle + 1
break
elif sorted_list[middle] < item:
left = middle + 1
else:
right = middle - 1
sorted_list.insert(left, item)
return sorted_list
def sortlist_2d(list_2d):
def merge(left, right):
result = []
while left and right:
if left[0][0] < right[0][0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
return result + left + right
length = len(list_2d)
if length <= 1:
return list_2d
middle = length // 2
return merge(sortlist_2d(list_2d[:middle]), sortlist_2d(list_2d[middle:]))
if len(collection) <= 1:
return collection
"""
Group the items into two pairs, and leave one element if there is a last odd item.
Example: [999, 100, 75, 40, 10000]
-> [999, 100], [75, 40]. Leave 10000.
"""
two_paired_list = []
has_last_odd_item = False
for i in range(0, len(collection), 2):
if i == len(collection) - 1:
has_last_odd_item = True
else:
"""
Sort two-pairs in each groups.
Example: [999, 100], [75, 40]
-> [100, 999], [40, 75]
"""
if collection[i] < collection[i + 1]:
two_paired_list.append([collection[i], collection[i + 1]])
else:
two_paired_list.append([collection[i + 1], collection[i]])
"""
Sort two_paired_list.
Example: [100, 999], [40, 75]
-> [40, 75], [100, 999]
"""
sorted_list_2d = sortlist_2d(two_paired_list)
"""
40 < 100 is sure because it has already been sorted.
Generate the sorted_list of them so that you can avoid unnecessary comparison.
Example:
group0 group1
40 100
75 999
->
group0 group1
[40, 100]
75 999
"""
result = [i[0] for i in sorted_list_2d]
"""
100 < 999 is sure because it has already been sorted.
Put 999 in last of the sorted_list so that you can avoid unnecessary comparison.
Example:
group0 group1
[40, 100]
75 999
->
group0 group1
[40, 100, 999]
75
"""
result.append(sorted_list_2d[-1][1])
"""
Insert the last odd item left if there is.
Example:
group0 group1
[40, 100, 999]
75
->
group0 group1
[40, 100, 999, 10000]
75
"""
if has_last_odd_item:
pivot = collection[-1]
result = binary_search_insertion(result, pivot)
"""
Insert the remaining items.
In this case, 40 < 75 is sure because it has already been sorted.
Therefore, you only need to insert 75 into [100, 999, 10000],
so that you can avoid unnecessary comparison.
Example:
group0 group1
[40, 100, 999, 10000]
^ You don't need to compare with this as 40 < 75 is already sure.
75
->
[40, 75, 100, 999, 10000]
"""
is_last_odd_item_inserted_before_this_index = False
for i in range(len(sorted_list_2d) - 1):
if result[i] == collection[-i]:
is_last_odd_item_inserted_before_this_index = True
pivot = sorted_list_2d[i][1]
# If last_odd_item is inserted before the item's index,
# you should forward index one more.
if is_last_odd_item_inserted_before_this_index:
result = result[: i + 2] + binary_search_insertion(result[i + 2 :], pivot)
else:
result = result[: i + 1] + binary_search_insertion(result[i + 1 :], pivot)
return result
nums = [4, 3, 5, 1, 2]
print("\nOriginal list:")
print(nums)
print("After applying Merge-insertion Sort the said list becomes:")
print(merge_insertion_sort(nums))
print(nums)
nums = [5, 9, 10, 3, -4, 5, 178, 92, 46, -18, 0, 7]
print("\nOriginal list:")
print(nums)
print("After applying Merge-insertion Sort the said list becomes:")
print(merge_insertion_sort(nums))
print(nums)
nums = [1.1, 1, 0, -1, -1.1, .1]
print("\nOriginal list:")
print(nums)
print("After applying Merge-insertion Sort the said list becomes:")
print(merge_insertion_sort(nums))
chars = ['z','a','y','b','x','c']
print("\nOriginal list:")
print(chars)
print("After applying Merge-insertion Sort the said list becomes:")
print(merge_insertion_sort(chars))
Sample Output:
Original list: [4, 3, 5, 1, 2] After applying Merge-insertion Sort the said list becomes: [1, 2, 3, 4, 5] [4, 3, 5, 1, 2] Original list: [5, 9, 10, 3, -4, 5, 178, 92, 46, -18, 0, 7] After applying Merge-insertion Sort the said list becomes: [-18, -4, 0, 3, 5, 5, 7, 9, 10, 46, 92, 178] [5, 9, 10, 3, -4, 5, 178, 92, 46, -18, 0, 7] Original list: [1.1, 1, 0, -1, -1.1, 0.1] After applying Merge-insertion Sort the said list becomes: [-1.1, -1, 0, 0.1, 1, 1.1] Original list: ['z', 'a', 'y', 'b', 'x', 'c'] After applying Merge-insertion Sort the said list becomes: ['a', 'b', 'c', 'x', 'y', 'z']
Flowchart:
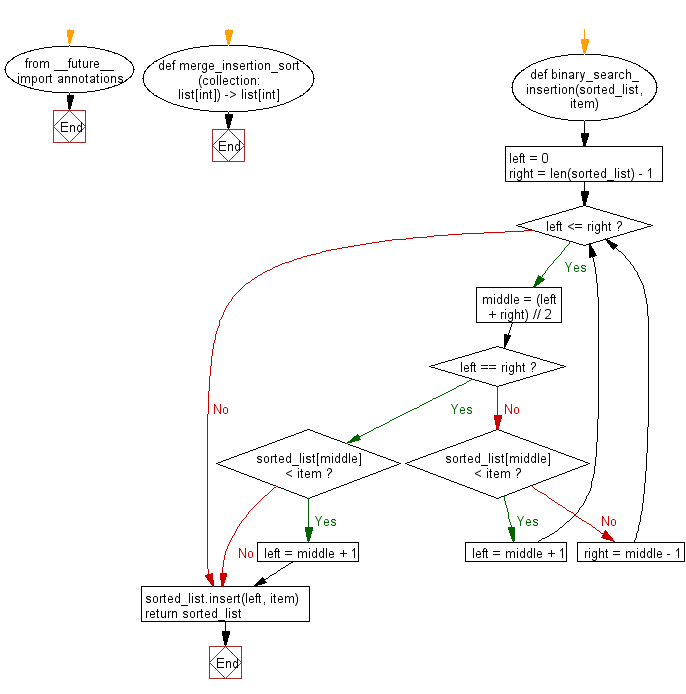
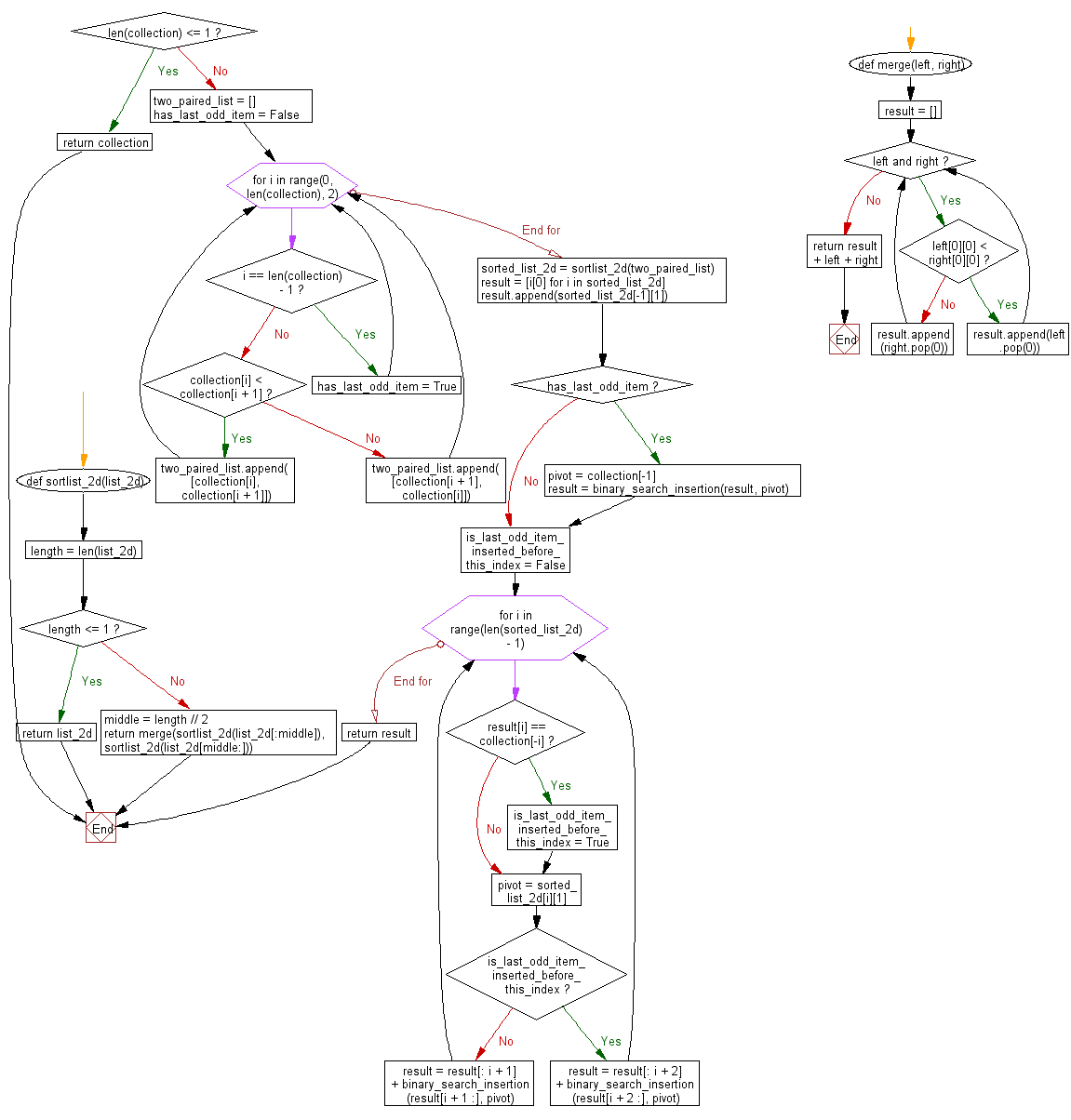

For more Practice: Solve these Related Problems:
- Write a Python program to implement merge-insertion sort and print the number of comparisons made during the sort.
- Write a Python script to sort a list using merge-insertion sort and then display the intermediate merged lists.
- Write a Python program to implement merge-insertion sort on a list of integers and compare its performance with standard merge sort.
- Write a Python function to perform merge-insertion sort and then verify the result by checking against Python’s sorted() output.
Go to:
Previous: Write a Python program to sort unsorted strings using natural sort.
Next: Python Linked List Exercise Home.
Python Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
