Python List Advanced Exercise - Find the k^th smallest element in a list

Python List Advanced: Exercise-4 with Solution

Write a Python function to find the k^th smallest element in a list.

Sample Solution-1:

This function sorts the list ascending. Since Python list indexing starts with 0, and returns the (k-1)^th element. This approach has a time complexity of O(n log n) due to the sorting operation

Python Code:

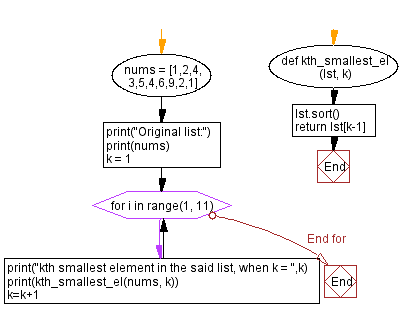
 # Define a function to find the kth smallest element in a list
def kth_smallest_el(lst, k):
    # Sort the list in ascending order
    lst.sort()
    # Return the kth smallest element (0-based index, so k-1)
    return lst[k - 1]

# Create a list of numbers
nums = [1, 2, 4, 3, 5, 4, 6, 9, 2, 1]

# Print the original list
print("Original list:")
print(nums)

# Initialize 'k' to 1
k = 1

# Iterate from k = 1 to k = 10
for i in range(1, 11):
    # Print a message indicating the value of 'k'
    print("kth smallest element in the said list, when k =", k)
    
    # Call the kth_smallest_el function with 'k' and print the result
    print(kth_smallest_el(nums, k))
    
    # Increment 'k' by 1 for the next iteration
    k = k + 1

Sample Output:

Original list:
[1, 2, 4, 3, 5, 4, 6, 9, 2, 1]
kth smallest element in the said list, when k =  1
1
kth smallest element in the said list, when k =  2
1
kth smallest element in the said list, when k =  3
2
kth smallest element in the said list, when k =  4
2
kth smallest element in the said list, when k =  5
3
kth smallest element in the said list, when k =  6
4
kth smallest element in the said list, when k =  7
4
kth smallest element in the said list, when k =  8
5
kth smallest element in the said list, when k =  9
6
kth smallest element in the said list, when k =  10
9

Flowchart:

What is the time complexity and space complexity of the following Python code?

def kth_smallest_el(lst, k):
    lst.sort()
    return lst[k-1]

Time complexity - The code uses the built-in Python sort() function, which has a time complexity of O(n log n), and then retrieves the kth smallest element, which takes constant time. So, the time complexity of the given code is O(n log n), where n is the length of the input list "lst".

Space complexity - The space complexity of the code is O(1), as the code only uses a constant amount of additional space regardless of the size of the input list "lst".

Sample Solution-2:

In computer science, quickselect is a selection algorithm to find the kth smallest element in an unordered list, also known as the k^th order statistic. Like the related quicksort sorting algorithm, it was developed by Tony Hoare, and thus is also known as Hoare's selection algorithm.
Here is an implementation of the k^th smallest element in a list using the QuickSelect algorithm:

Python Code:

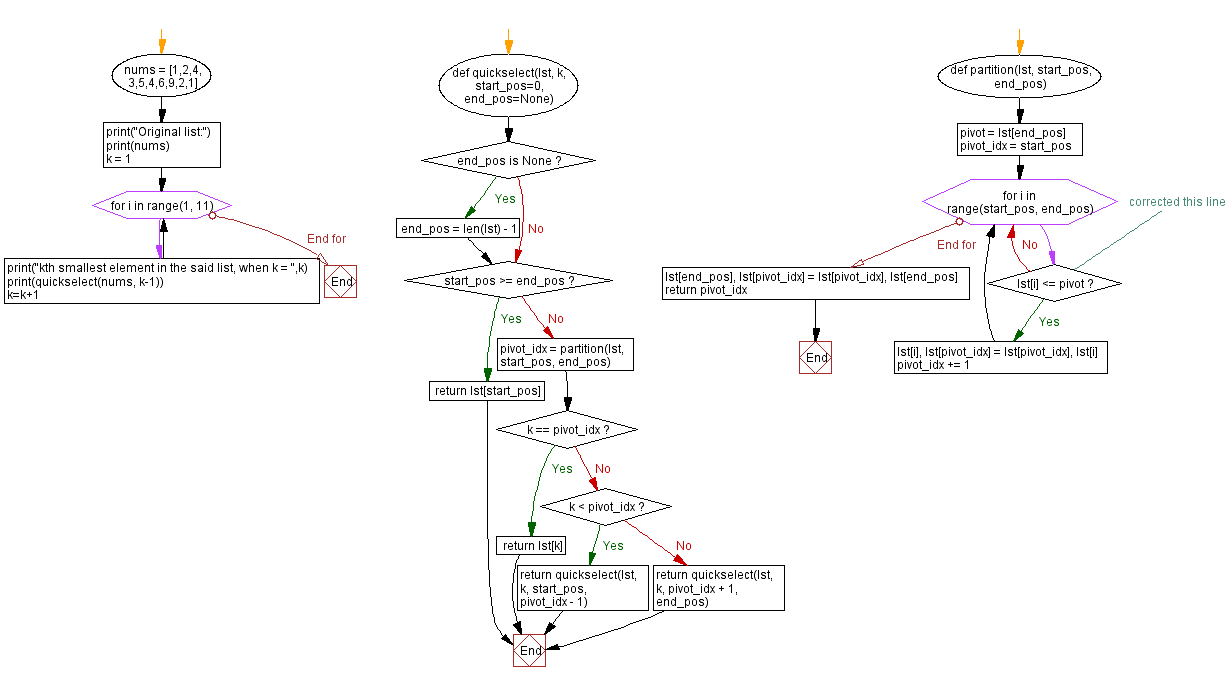
# Define a function to find the kth smallest element in a list using quickselect algorithm
def quickselect(lst, k, start_pos=0, end_pos=None):
    # If end_pos is not specified, set it to the last index of the list
    if end_pos is None:
        end_pos = len(lst) - 1

    # Base case: If the start position is greater than or equal to the end position, return the element at the start position
    if start_pos >= end_pos:
        return lst[start_pos]

    # Find the pivot index using the partition function
    pivot_idx = partition(lst, start_pos, end_pos)

    # Compare k with the pivot index to determine which side to search for the kth smallest element
    if k == pivot_idx:
        return lst[k]
    elif k < pivot_idx:
        # Recursively search for the kth smallest element in the left part of the partition
        return quickselect(lst, k, start_pos, pivot_idx - 1)
    else:
        # Recursively search for the kth smallest element in the right part of the partition
        return quickselect(lst, k, pivot_idx + 1, end_pos)

# Define a function to partition a list and choose a pivot element
def partition(lst, start_pos, end_pos):
    # Choose the pivot element as the last element in the list
    pivot = lst[end_pos]
    pivot_idx = start_pos

    # Iterate through the list and move elements smaller than the pivot to the left side
    for i in range(start_pos, end_pos):
        if lst[i] <= pivot:  # Compare elements with the pivot
            lst[i], lst[pivot_idx] = lst[pivot_idx], lst[i]
            pivot_idx += 1

    # Swap the pivot element to its correct position in the partition
    lst[end_pos], lst[pivot_idx] = lst[pivot_idx], lst[end_pos]

    # Return the pivot index
    return pivot_idx

# Create a list of numbers
nums = [1, 2, 4, 3, 5, 4, 6, 9, 2, 1]

# Print the original list
print("Original list:")
print(nums)

# Initialize 'k' to 1
k = 1

# Iterate from k = 1 to k = 10
for i in range(1, 11):
    # Print a message indicating the value of 'k'
    print("kth smallest element in the said list, when k =", k)
    
    # Call the quickselect function with 'k-1' to find the kth smallest element and print the result
    print(quickselect(nums, k - 1))
    
    # Increment 'k' by 1 for the next iteration
    k = k + 1

Sample Output:

Original list:
[1, 2, 4, 3, 5, 4, 6, 9, 2, 1]
kth smallest element in the said list, when k =  1
1
kth smallest element in the said list, when k =  2
1
kth smallest element in the said list, when k =  3
2
kth smallest element in the said list, when k =  4
2
kth smallest element in the said list, when k =  5
3
kth smallest element in the said list, when k =  6
4
kth smallest element in the said list, when k =  7
4
kth smallest element in the said list, when k =  8
5
kth smallest element in the said list, when k =  9
6
kth smallest element in the said list, when k =  10
9

Flowchart:

What is the time complexity and space complexity of the following Python code?

def quickselect(lst, k, start_pos=0, end_pos=None):
    if end_pos is None:
        end_pos = len(lst) - 1
    if start_pos >= end_pos:
        return lst[start_pos]
    pivot_idx = partition(lst, start_pos, end_pos)
    if k == pivot_idx:
        return lst[k]
    elif k < pivot_idx:
        return quickselect(lst, k, start_pos, pivot_idx - 1)
    else:
        return quickselect(lst, k, pivot_idx + 1, end_pos)
def partition(lst, start_pos, end_pos):
    pivot = lst[end_pos]
    pivot_idx = start_pos
    for i in range(start_pos, end_pos):
        if lst[i] <= pivot: # corrected this line
            lst[i], lst[pivot_idx] = lst[pivot_idx], lst[i]
            pivot_idx += 1
    lst[end_pos], lst[pivot_idx] = lst[pivot_idx], lst[end_pos]
    return pivot_idx

Time complexity - The code uses the quickselect algorithm to find the kth smallest element in the list "lst", which has an average time complexity of O(n) and a worst-case time complexity of O(n^2). However, the worst-case time complexity is highly unlikely due to the randomized nature of the algorithm. So, the time complexity of the given code is O(n), where n is the length of the input list "lst".

Space complexity - The code uses recursion to call the quickselect function multiple times with smaller sub-arrays. The maximum recursion depth is logarithmic in n, so the space complexity is O(log n). Additionally, the "partition" function uses a constant amount of additional space, so it does not contribute to the space complexity.

Python Code Editor:

Previous: Permutations of the members of a list.
Next: Find the k^th smallest element in a list.