C Exercises: Get the kth permutation sequence from two given integers n and k

Last update on August 07 2025 12:49:22 (UTC/GMT +8 hours)

5. Kth Permutation Sequence Variants

The following set contains a total of n! unique permutations
Set: [1, 2, 3, ..., n]
If n =3 we will get the following sequence:
1. "123"
2. "132"
3. "213"
4. "231"
5. "312"
6. "321"
Input: n = 3, k = 4
Output: "231"
Write a C program to get the kth permutation sequence from two given integers n and k. In these integers, n is between 1 and 9 inclusive. In addition, k is between 1 and n! Inclusive.

Example:
Input:
n = 3
int k = 2

n = 4
k = 7
Output:
Kth sequence: 132
Kth sequence: 2134

Sample Solution:

C Code:

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// Function to calculate factorial of a number
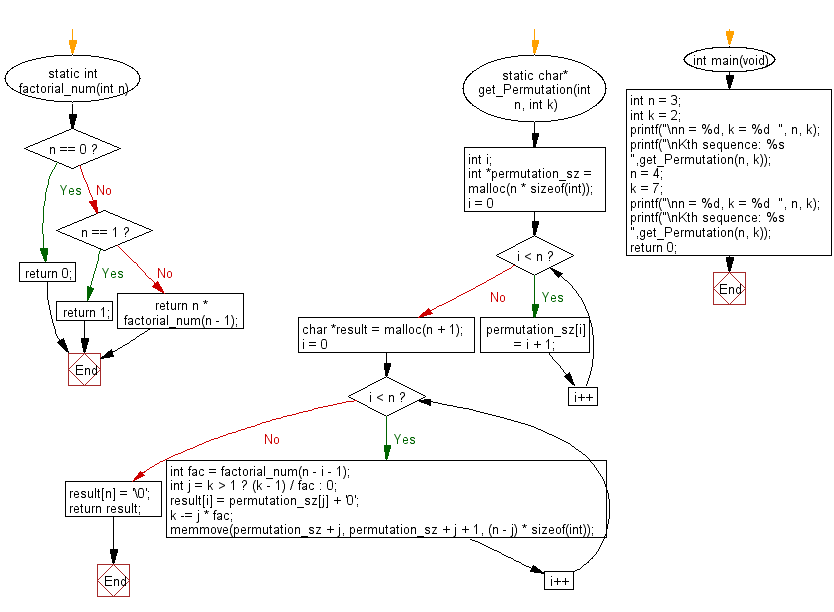
static int factorial_num(int n) {
    if (n == 0) {
        return 0;
    } else if (n == 1) {
        return 1;
    } else {
        return n * factorial_num(n - 1);
    }
}

// Function to get the kth permutation sequence of size n
static char* get_Permutation(int n, int k) {
    int i;

    // Create an array to store permutation elements from 1 to n
    int *permutation_sz = malloc(n * sizeof(int));
    for (i = 0; i < n; i++) {
        permutation_sz[i] = i + 1;
    }

    // Allocate memory to store the resulting permutation sequence
    char *result = malloc(n + 1);

    for (i = 0; i < n; i++) {
        int fac = factorial_num(n - i - 1); // Calculate factorial of (n - i - 1)

        // Calculate index for the current position in the permutation
        int j = k > 1 ? (k - 1) / fac : 0;

        // Get the permutation element at index j and store it in the result
        result[i] = permutation_sz[j] + '0';

        // Update k and adjust the permutation array
        k -= j * fac;
        memmove(permutation_sz + j, permutation_sz + j + 1, (n - j) * sizeof(int));
    }

    result[n] = '\0'; // Add null terminator to the resulting string
    return result;   // Return the resulting permutation sequence
}

int main(void)
{
    // Test case 1
    int n = 3;
    int k = 2;
    printf("\nn = %d, k = %d  ", n, k);
    printf("\nKth sequence: %s ", get_Permutation(n, k));

    // Test case 2
    n = 4;
    k = 7;
    printf("\nn = %d, k = %d  ", n, k);
    printf("\nKth sequence: %s ", get_Permutation(n, k));

    return 0;
}

Sample Output:

n = 3, k = 2  
Kth sequence: 132 
n = 4, k = 7  
Kth sequence: 2134

Flowchart:

$Flowchart: Get the kth permutation sequence from two given integers n and k.$

For more Practice: Solve these Related Problems:

Write a C program to generate the kth permutation sequence of numbers 1 to n using recursion and backtracking.
Write a C program to calculate the kth permutation directly using factorial number system without generating all permutations.
Write a C program to generate the kth lexicographic permutation with iterative swapping techniques.
Write a C program to find the kth permutation sequence and validate it by comparing with the complete permutation list.

Go to:

PREV : Power Function Variants.
NEXT : Decimal Number String Check Variants.

C Programming Code Editor:

Improve this sample solution and post your code through Disqus.