C++ Exercises: Find the number of perfect square numbers which represent a sum of a given number

Last update on August 19 2025 05:35:50 (UTC/GMT +8 hours)

27. Count Perfect Squares Summing to a Given Number

Write a C++ program to find the number of perfect squares (e.g. 1, 4, 9, 16, ...) that represent the sum of a given number.

Sample Input: n = 5
Number of perfect square whose sum equal to 5 = 2
Sample Input: n = 7
Number of perfect square whose sum equal to 7 = 4

Sample Solution:

C++ Code :

#include <iostream>
#include <vector>

using namespace std;

// Function to find the minimum number of perfect square numbers that sum up to n
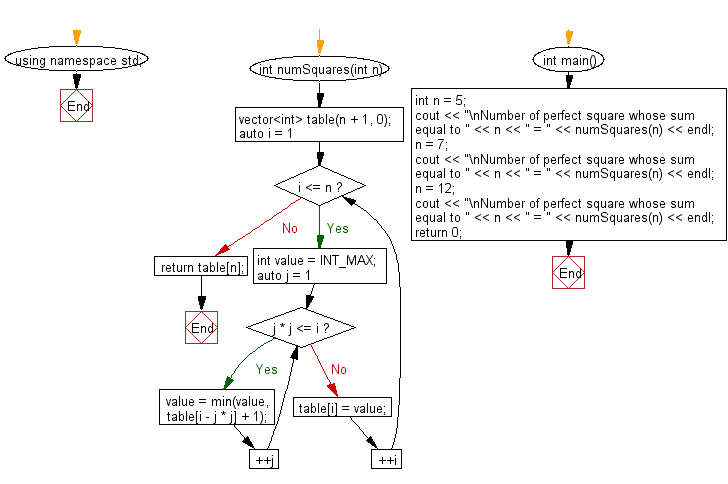
int numSquares(int n) {
    // Create a vector 'table' of size (n + 1) initialized with 0
    vector<int> table(n + 1, 0);

    // Loop from 1 to n
    for (auto i = 1; i <= n; ++i) {
        int value = INT_MAX; // Initialize 'value' as the maximum integer value

        // Loop through squares from 1 to sqrt(i)
        for (auto j = 1; j * j <= i; ++j) {
            // Update 'value' by finding the minimum among the current 'value' and
            // the value at table[i - j * j] plus 1
            value = min(value, table[i - j * j] + 1);
        }

        // Store the minimum number of perfect square numbers that sum up to 'i' in 'table'
        table[i] = value;
    }

    return table[n]; // Return the minimum number of perfect square numbers that sum up to 'n'
}

int main() {
    int n = 5;  // (4 + 1)
    cout << "\nNumber of perfect squares whose sum equals " << n << " = " << numSquares(n) << endl;

    n = 7;  // (4 + 1 + 1 + 1)
    cout << "\nNumber of perfect squares whose sum equals " << n << " = " << numSquares(n) << endl;

    n = 12;  // (4 + 4 + 4)
    cout << "\nNumber of perfect squares whose sum equals " << n << " = " << numSquares(n) << endl;

    return 0;
}

Sample Output:

Number of perfect square whose sum equal to 5 = 2

Number of perfect square whose sum equal to 7 = 4

Number of perfect square whose sum equal to 12 = 3

Flowchart:

$Flowchart: Find the number of perfect square numbers which represent a sum of a given number.$

For more Practice: Solve these Related Problems:

Write a C++ program to count the number of ways a given number can be expressed as the sum of perfect squares using recursion.
Write a C++ program that finds the number of combinations of perfect squares that add up to a given number using dynamic programming.
Write a C++ program to recursively determine the count of perfect square combinations that sum to a target value.
Write a C++ program that calculates the number of ways to represent a number as the sum of perfect squares and prints the count.

Go to:

PREV : Find the Missing Number in a Sequence.
NEXT : Maximum Product from Breaking an Integer.

C++ Code Editor:

Contribute your code and comments through Disqus.