Java: Find the length of the longest consecutive sequence path of a given binary tree

Last update on May 14 2025 12:59:31 (UTC/GMT +8 hours)

Longest Consecutive Path in Tree

Write a Java program to find the length of the longest consecutive sequence path in a given binary tree.

Note: The longest consecutive path need to be from parent to child.

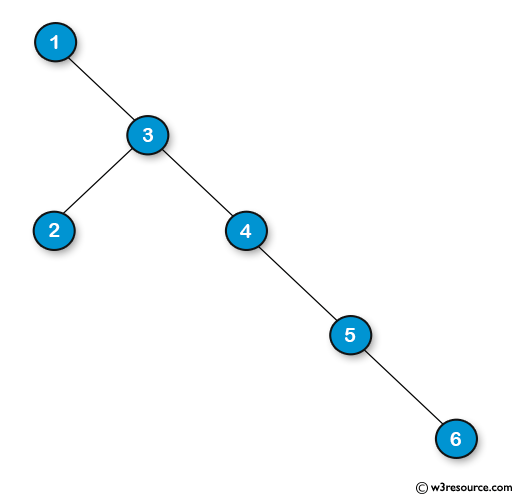
Sample Binary tree:

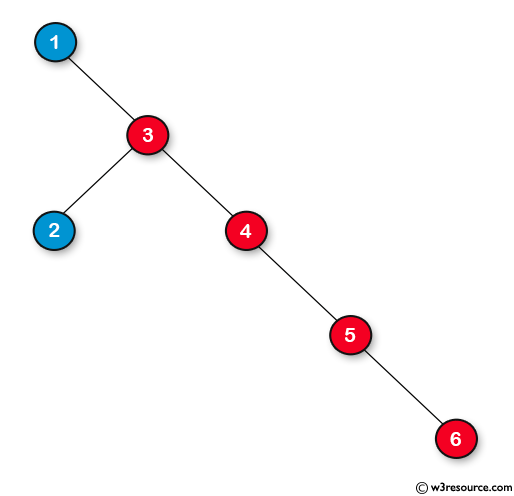
Result:

Sample Solution:

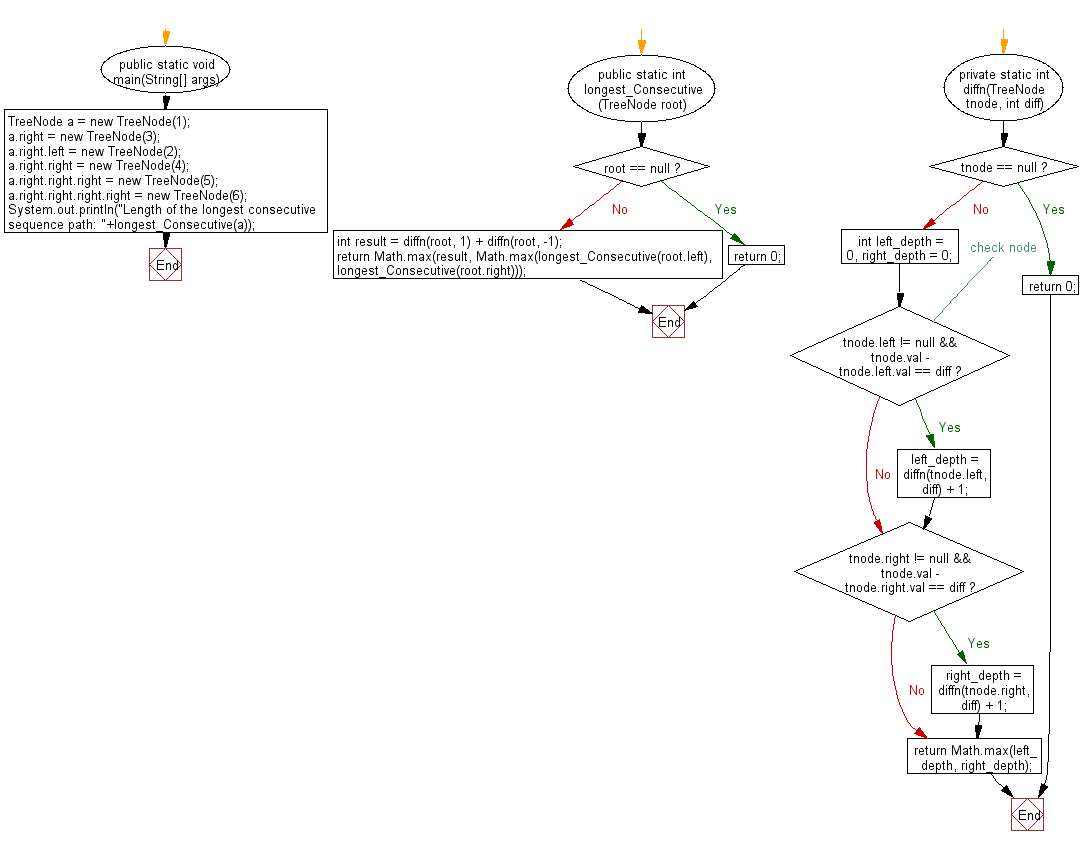
Java Code:

// Importing necessary Java utilities
import java.util.*;

// TreeNode class definition
class TreeNode {
    public int val;
    public TreeNode left, right;

    // TreeNode class constructor
    public TreeNode(int val) {
        this.val = val;
        this.left = this.right = null;
    }
}

// Main class Solution
public class Solution {
    // Main method
    public static void main(String[] args) {
        // Creating the tree nodes and constructing the binary tree
        TreeNode a = new TreeNode(1);
        a.right = new TreeNode(3);
        a.right.left = new TreeNode(2);
        a.right.right = new TreeNode(4);
        a.right.right.right = new TreeNode(5);
        a.right.right.right.right = new TreeNode(6);

        // Printing the length of the longest consecutive sequence path
        System.out.println("Length of the longest consecutive sequence path: " + longest_Consecutive(a));
    }

    // Method to find the longest consecutive sequence path in a binary tree
    public static int longest_Consecutive(TreeNode root) {
        // Base case: if the root is null, return 0
        if (root == null) {
            return 0;
        }

        // Compute the result by recursively traversing the tree
        int result = diffn(root, 1) + diffn(root, -1);
        return Math.max(result, Math.max(longest_Consecutive(root.left), longest_Consecutive(root.right)));
    }

    // Helper method to compute the depth of the consecutive sequence path
    private static int diffn(TreeNode tnode, int diff) {
        // Base case: if the tree node is null, return 0
        if (tnode == null) {
            return 0;
        }

        // Initialize depths for left and right subtrees
        int left_depth = 0, right_depth = 0;

        // Check if there exists a consecutive sequence path in left and right subtrees
        if (tnode.left != null && tnode.val - tnode.left.val == diff) {
            left_depth = diffn(tnode.left, diff) + 1;
        }
        if (tnode.right != null && tnode.val - tnode.right.val == diff) {
            right_depth = diffn(tnode.right, diff) + 1;
        }

        // Return the maximum depth among left and right consecutive sequence paths
        return Math.max(left_depth, right_depth);
    }
} 

Sample Output:

Length of the longest consecutive sequence path:  4

Flowchart:

For more Practice: Solve these Related Problems:

• Write a Java program to find the longest consecutive sequence in a binary tree that can extend in both upward and downward directions.
• Write a Java program to determine the longest increasing path (not necessarily consecutive) in a binary tree.
• Write a Java program to find the longest path in a binary tree where node values increase consecutively, allowing gaps of exactly one.
• Write a Java program to compute the longest consecutive decreasing sequence in a binary tree from parent to child.

Go to:

• Java Basic Part-II Programming Exercises Home ↩
• Java Exercises Home ↩

PREV : Sum Digits to Single Digit.
NEXT : Check Isomorphic Strings.

Java Code Editor:

Company:  Google NetEase

Contribute your code and comments through Disqus.