Java: Calculate e raise to the power x using sum of first n terms of Taylor Series

Last update on May 15 2025 13:08:26 (UTC/GMT +8 hours)

Taylor Series for e^x

From Wikipedia,
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point.
Example:
The Taylor series for any polynomial is the polynomial itself.

The above expansion holds because the derivative of e^x with respect to x is also e^x, and e⁰ equals 1.
This leaves the terms (x − 0)ⁿ in the numerator and n! in the denominator for each term in the infinite sum.
Write a Java program to calculate e raise to the power x using the sum of the first n terms of the Taylor Series.

Sample Solution:

Java Code:

import java.util.*;

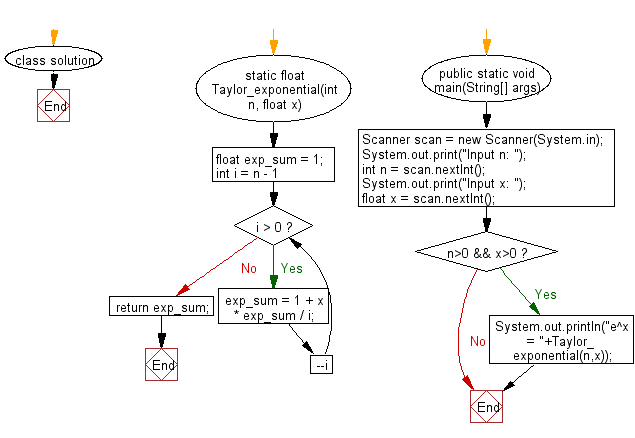
class solution {

   static float Taylor_exponential(int n, float x) 
    { 
        float exp_sum = 1;  
   
        for (int i = n - 1; i > 0; --i ) 
            exp_sum = 1 + x * exp_sum / i; 
   
        return exp_sum; 
    } 

    public static void main(String[] args)
    {   
       Scanner scan = new Scanner(System.in);
       System.out.print("Input n: ");
       int n = scan.nextInt();
	   System.out.print("Input x: ");
       float x = scan.nextInt();
       if (n>0 && x>0)
		{	
		 System.out.println("e^x = "+Taylor_exponential(n,x)); 
		}         
   }
}

Sample Output:

Input n:  25
Input x:  5
e^x = 148.41316

Flowchart:

For more Practice: Solve these Related Problems:

• Write a Java program to approximate e^x using the Taylor Series recursively with a given tolerance for convergence.
• Write a Java program to compute e^x using an iterative Taylor Series method and compare the result with Math.exp(x).
• Write a Java program to implement the Taylor Series for e^x using Java streams to process the series terms.
• Write a Java program to calculate e^x using a recursive Taylor Series algorithm and then compute the error percentage relative to the built-in function.

Go to:

• Java Math Exercises Home ↩
• Java Exercises Home ↩

PREV : Calculate Binomial Coefficient.
NEXT : Prime Factors of Number.

Java Code Editor:

Contribute your code and comments through Disqus.