Java: Classify Abundant, deficient and perfect number (integers) between 1 to 10,000

Last update on March 11 2025 11:10:49 (UTC/GMT +8 hours)

Categorize Numbers: Abundant, Deficient, Perfect

Write a Java program that categorizes integers between 1 and 10,000 as Abundant, Deficient, and Perfect.

In number theory, an abundant number is a number for which the sum of its proper divisors is greater than the number itself.
Example :
The first few abundant numbers are:
12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100, 102,…
The integer 12 is the first abundant number. Its proper divisors are 1, 2, 3, 4 and 6 for a total of 16.
Deficient number: In number theory, a deficient number is a number n for which the sum of divisors σ(n)<2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)<n. The value 2n − σ(n) (or n − s(n)) is called the number's deficiency.
As an example, divisors of 21 are 1, 3 and 7, and their sum is 11. Because 11 is less than 21, the number 21 is deficient. Its deficiency is 2 × 21 − 32 = 10.
The first few deficient numbers are:
1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, …….
Perfect number: In number system, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself.
Equivalently, a perfect number is a number that is half the sum of all of its positive divisors (including itself) i.e. σ1(n) = 2n.
The first perfect number is 6. Its proper divisors are 1, 2, and 3, and 1 + 2 + 3 = 6. Equivalently, the number 6 is equal to half the sum of all its positive divisors: ( 1 + 2 + 3 + 6 ) / 2 = 6. The next perfect number is 28 = 1 + 2 + 4 + 7 + 14. This is followed by the perfect numbers 496 and 8128.

Pictorial Presentation:

Sample Solution:

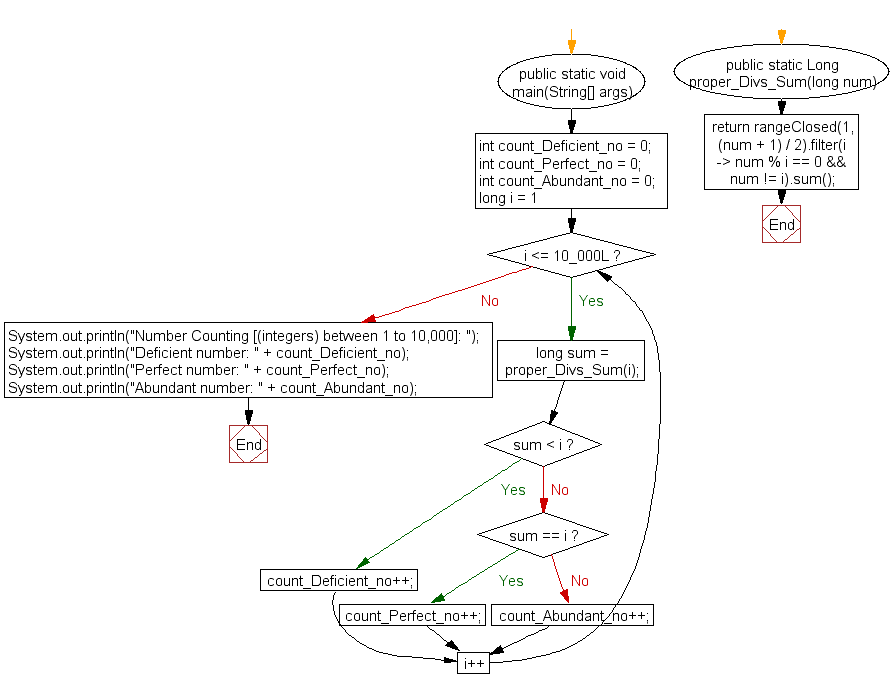
Java Code:

import static java.util.stream.LongStream.rangeClosed;
public class Exercise2 {
    
   public static void main(String[] args) {
        int count_Deficient_no = 0;
        int count_Perfect_no = 0;
        int count_Abundant_no = 0;
 
        for (long i = 1; i <= 10_000L; i++) {
            long sum = proper_Divs_Sum(i);
            if (sum < i)
                count_Deficient_no++;
            else if (sum == i)
                count_Perfect_no++;
            else
                count_Abundant_no++;
        }
        System.out.println("Number Counting [(integers) between 1 to 10,000]: ");
        System.out.println("Deficient number: " + count_Deficient_no);
        System.out.println("Perfect number: " + count_Perfect_no);
        System.out.println("Abundant number: " + count_Abundant_no);
    }
     public static Long proper_Divs_Sum(long num) {
        return rangeClosed(1, (num + 1) / 2).filter(i -> num % i == 0 && num != i).sum();
    }
}

Sample Output:

Number Counting [(integers) between 1 to 10,000]:                                                             
Deficient number: 7508                                                                                        
Perfect number: 4                                                                                             
Abundant number: 2488

Flowchart:

For more Practice: Solve these Related Problems:

• Write a Java program to compute the sum of proper divisors for numbers in a range recursively and classify each as abundant, deficient, or perfect.
• Write a Java program to find the smallest abundant number greater than a given input using iterative search.
• Write a Java program to count and list abundant, deficient, and perfect numbers from an array using Java streams.
• Write a Java program to optimize divisor sum calculations using memoization when categorizing numbers between 1 and 10,000.

Java Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Java program to check whether a given number is an ugly number.
Next: Write a Java program to generate random integers in a specific range.