Java: Generate and show all Kaprekar numbers less than 1000
Kaprekar Numbers < 1000
Write a Java program to generate and show all Kaprekar numbers less than 1000.
In number theory, a Kaprekar number for a given base is a non-negative integer, the representation of whose square in that base can be split into two parts that add up to the original number again. For instance, 45 is a Kaprekar number, because 452 = 2025 and 20 + 25 = 45.
The first few Kaprekar numbers in base 10 are:
1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, …
Pictorial Presentation:
Sample Solution:
Java Code:
public class Example4 {
public static void main(String[] args){
int ctr = 0;
int base = (args.length > 0) ? Integer.parseInt(args[0]) : 10;
for(long n = 1; n <= 1000; n++){
String sqr_Str = Long.toString(n * n, base);
for(int j = 0; j < sqr_Str.length() / 2 + 1; j++){
String[] parts = split_num(sqr_Str, j);
long first_Num = Long.parseLong(parts[0], base);
long sec_Num = Long.parseLong(parts[1], base);
if(sec_Num == 0) break;
if(first_Num + sec_Num == n){
System.out.println(Long.toString(n, base) +
"\t" + sqr_Str + "\t " + parts[0] + " + " + parts[1]);
ctr++;
break;
}
}
}
System.out.println(ctr + " Kaprekar numbers.");
}
private static String[] split_num(String str, int idx){
String[] ans1 = new String[2];
ans1[0] = str.substring(0, idx);
if(ans1[0].equals("")) ans1[0] = "0";
ans1[1] = str.substring(idx);
return ans1;
}
}
Sample Output:
1 1 0 + 1 9 81 8 + 1 45 2025 20 + 25 55 3025 30 + 25 99 9801 98 + 01 297 88209 88 + 209 703 494209 494 + 209 999 998001 998 + 001 8 Kaprekar numbers.
Flowchart:
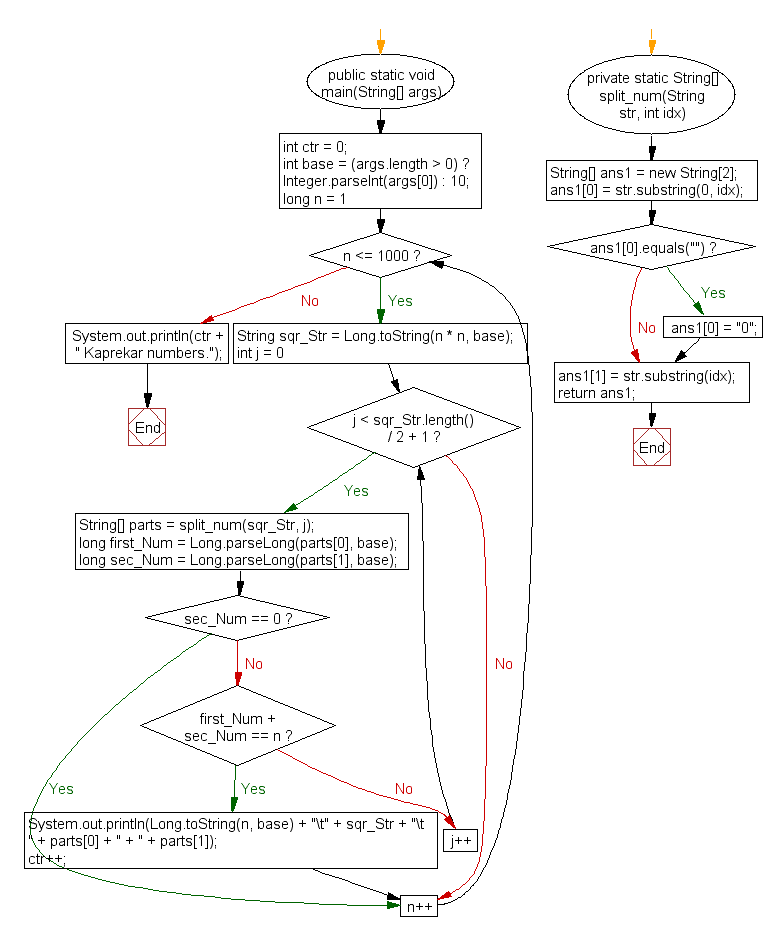
For more Practice: Solve these Related Problems:
- Write a Java program to generate Kaprekar numbers within a specified range by splitting the square of the number in all possible ways.
- Write a Java program to identify the next Kaprekar number after a given number using iterative search.
- Write a Java program to test the Kaprekar property using both arithmetic and string manipulation methods.
- Write a Java program to optimize Kaprekar number detection by skipping non-candidate numbers based on their digit count.
Go to:
PREV : Generate Random Integers in Range.
NEXT : Seed Lychrel Numbers.
Java Code Editor:
Contribute your code and comments through Disqus.
What is the difficulty level of this exercise?
Test your Programming skills with w3resource's quiz.
