Python: Solve the specified equation

Last update on April 17 2025 13:05:52 (UTC/GMT +8 hours)

Solve Linear Equations

Write a Python program which solve the equation:
ax+by=c
dx+ey=f
Print the values of x, y where a, b, c, d, e and f are given.

Input:
a,b,c,d,e,f separated by a single space.
(-1,000 ≤ a,b,c,d,e,f ≤ 1,000)
Input the value of a, b, c, d, e, f:
5 8 6 7 9 4
Values of x and y:
-2.000 2.000

Sample Solution:

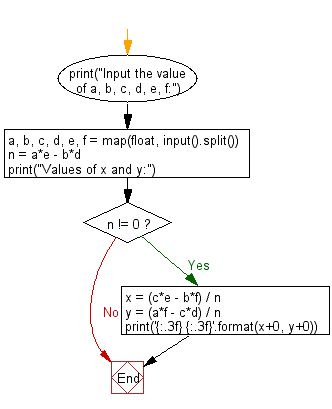
Python Code:

# Print statement to prompt the user to input the values of a, b, c, d, e, f
print("Input the value of a, b, c, d, e, f:")

# Using map and split to take six space-separated float values as input, then converting them to float
a, b, c, d, e, f = map(float, input().split())

# Calculating the determinant of the system of linear equations
n = a * e - b * d

# Print statement to display the values of x and y
print("Values of x and y:")

# Checking if the determinant is not zero to avoid division by zero
if n != 0:
    # Calculating the values of x and y using Cramer's rule
    x = (c * e - b * f) / n
    y = (a * f - c * d) / n

    # Printing the values of x and y with three decimal places
    print('{:.3f} {:.3f}'.format(x + 0, y + 0))

Sample Output:

Input the value of a, b, c, d, e, f:
 5 8 6 7 9 4
Values of x and y:
-2.000 2.000

Explanation:

The above Python code takes user input for six 'float' values representing coefficients of a system of linear equations. It then uses Cramer's rule to solve for the values of 'x' and 'y' in the system. The determinant of the coefficient matrix is calculated. If it's not zero, the values of 'x' and 'y' are determined and printed to three decimal places. If the determinant is zero, the code does not calculate the values, avoiding division by zero.

Flowchart:

For more Practice: Solve these Related Problems:

Write a Python program to solve a system of three linear equations with three variables.
Write a Python program to solve a system of two linear equations where one coefficient is given as a parameter.
Write a Python program to check whether two linear equations are independent or dependent.
Write a Python program to solve a system of linear equations using matrix inversion methods.

Go to:

Previous: Write a Python program to check whether three given lengths (integers) of three sides form a right triangle.
Next: Write a Python program to compute the amount of the debt in n months.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.