Python: Find the maximum sum of a contiguous subsequence from a given sequence of numbers a1, a2, a3, ... an

Last update on April 17 2025 13:01:31 (UTC/GMT +8 hours)

Max Subsequence Sum

Write a Python program to find the maximum sum of a contiguous subsequence from a given sequence of numbers a1, a2, a3, ... an. A subsequence of one element is also a continuous subsequence.

Input:
You can assume that 1 ≤ n ≤ 5000 and -100000 ≤ ai ≤ 100000.
Input numbers are separated by a space.
Input 0 to exit.
Input number of sequence of numbers you want to input (0 to exit): 3
Input numbers:
2
4
6
Maximum sum of the said contiguous subsequence:
12 Input number of sequence of numbers you want to input (0 to exit): 0

Sample Solution:

Python Code:

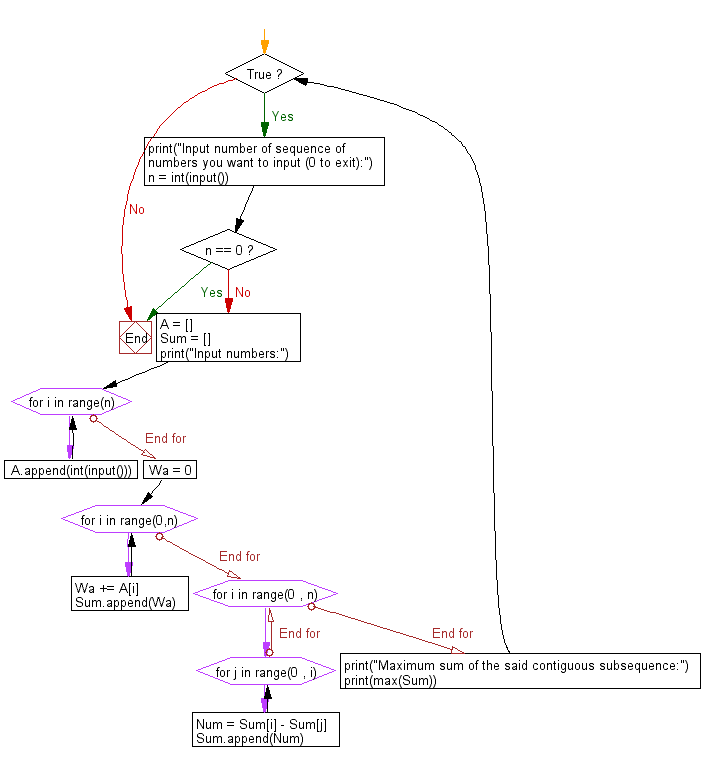
# Infinite loop to continuously receive input until the user enters 0
while True:
    # Prompt the user to input the number of sequence of numbers (0 to exit)
    print("Input number of sequence of numbers you want to input (0 to exit):")
    
    # Take user input for the number of sequences
    n = int(input())
    
    # Break the loop if the user enters 0
    if n == 0:
        break
    else:
        # Initialize empty lists A and Sum to store input numbers and cumulative sums
        A = []
        Sum = []
        
        # Prompt the user to input numbers for the sequence
        print("Input numbers:")
        
        # Take user input for the sequence of numbers
        for i in range(n):
            A.append(int(input()))
        
        # Calculate the cumulative sum of the sequence
        Wa = 0
        for i in range(0, n):
            Wa += A[i]
            Sum.append(Wa)
        
        # Generate all possible contiguous subsequences and add them to the Sum list
        for i in range(0, n):
            for j in range(0, i):
                Num = Sum[i] - Sum[j]
                Sum.append(Num)
        
        # Print the maximum sum of the contiguous subsequence
        print("Maximum sum of the said contiguous subsequence:")
        print(max(Sum))

Sample Output:

Input number of sequence of numbers you want to input (0 to exit):
 3
Input numbers:
 2
 4
 6
Maximum sum of the said contiguous subsequence:
12
Input number of sequence of numbers you want to input (0 to exit):
 0

Explanation:

Here is a breakdown of the above Python code:

First the code uses an infinite while loop to repeatedly receive input until the user enters 0.
It prompts the user to input the number of sequences and breaks the loop if the input is 0.
Inside the loop, it initializes empty lists A and Sum to store input numbers and cumulative sums.
It prompts the user to input numbers for the sequence and calculates the cumulative sum (Sum).
The code generates all possible contiguous subsequences and adds them to the Sum list.
It prints the maximum sum of the contiguous subsequence using the max function on the Sum list.

Flowchart:

For more Practice: Solve these Related Problems:

Write a Python program to find the contiguous subsequence within a sequence that has the maximum product.
Write a Python program to identify the contiguous subsequence with the minimum sum in a list of numbers.
Write a Python program to determine the maximum sum of a contiguous subsequence in a circular array.
Write a Python program to find the sum of the longest increasing contiguous subsequence within a sequence.

Go to:

Previous:Write a Python program to test whether two lines PQ and RS are parallel. The four points are P(x1, y1), Q(x2, y2), R(x3, y3), S(x4, y4).
Next: Write a python program to test if circumference of two circles intersect or overlap.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.