Python: Test if circumference of two circles intersect or overlap

Last update on April 17 2025 13:01:30 (UTC/GMT +8 hours)

Circle Overlap Checker

There are two circles C1 with radius r1, central coordinate (x1, y1) and C2 with radius r2 and central coordinate (x2, y2)

• "C2 is in C1" if C2 is in C1
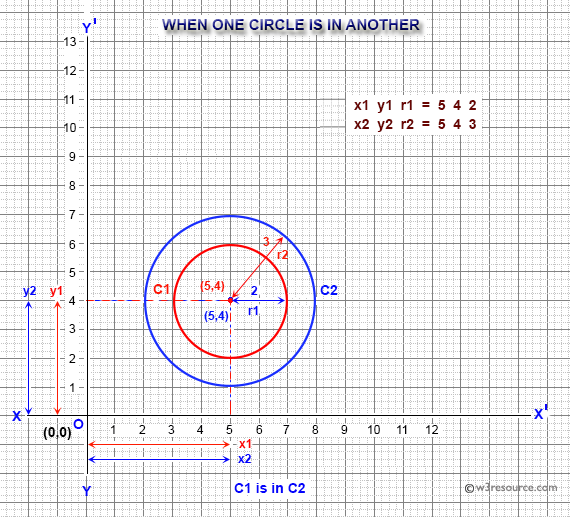
• "C1 is in C2" if C1 is in C2
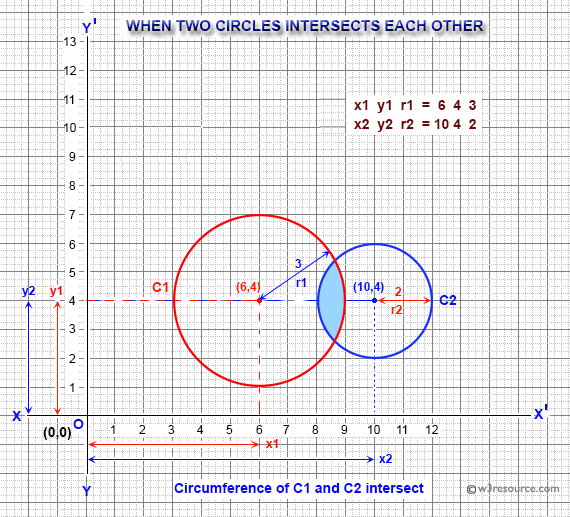
• "Circumference of C1 and C2 intersect" if circumference of C1 and C2 intersect
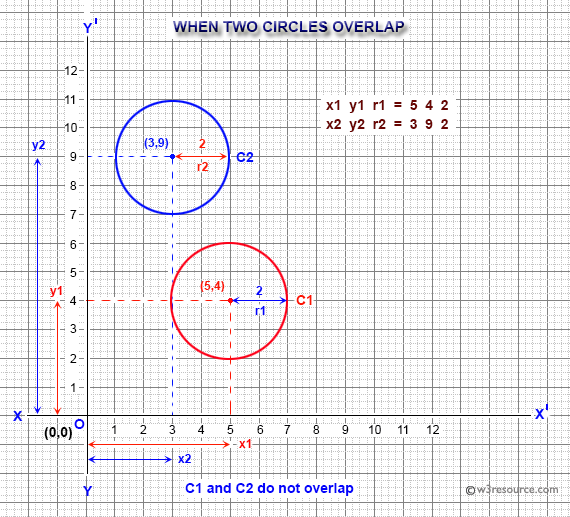
• "C1 and C2 do not overlap" if C1 and C2 do not overlap and
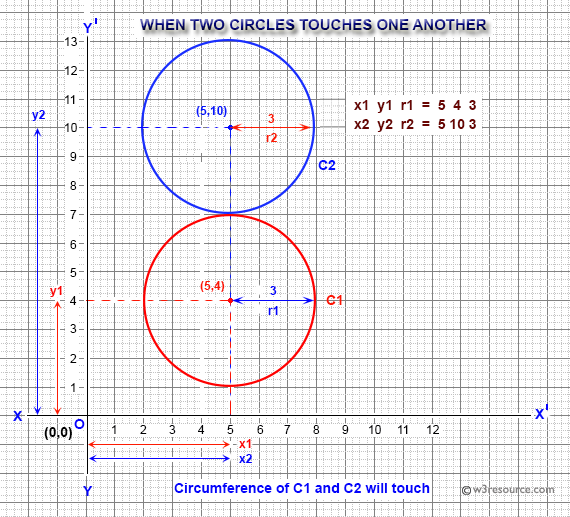
• "Circumference of C1 and C2 will touch" if C1 and C2 touch

Input:
Input numbers (real numbers) are separated by a space.

Visual Presentation:

Sample Solution:

Python Code:

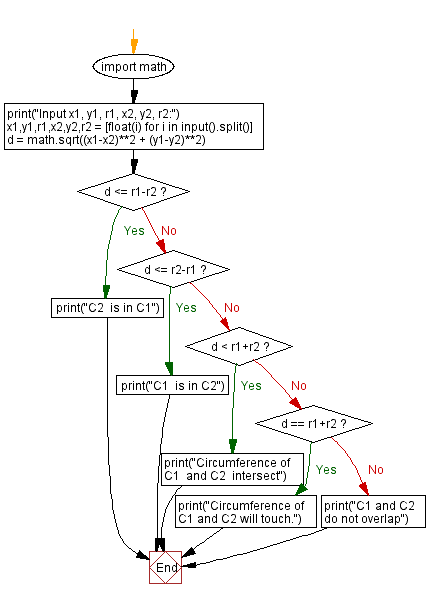
# Import the math module
import math

# Prompt the user to input x1, y1, r1, x2, y2, r2
print("Input x1, y1, r1, x2, y2, r2:")

# Take user input and convert it to floating-point numbers
x1, y1, r1, x2, y2, r2 = [float(i) for i in input().split()]

# Calculate the distance between the centers of the two circles
d = math.sqrt((x1 - x2)**2 + (y1 - y2)**2)

# Check and print the relationship between the two circles based on their radii and distance
if d <= r1 - r2:
    print("C2 is in C1")
elif d <= r2 - r1:
    print("C1 is in C2")
elif d < r1 + r2:
    print("Circumference of C1 and C2 intersect")
elif d == r1 + r2:
    print("Circumference of C1 and C2 will touch")
else:
    print("C1 and C2 do not overlap")

Sample Output:

Input x1, y1, r1, x2, y2, r2:
 5 4 2 3 9 2
C1 and C2  do not overlap

Input x1, y1, r1, x2, y2, r2:
 5 4 3 5 10 3
Circumference of C1 and C2 will touch

Input x1, y1, r1, x2, y2, r2:
 6 4 3 10 4 2
Circumference of C1  and C2  intersect

Input x1, y1, r1, x2, y2, r2:
 5 4 3 5 4 2
C2  is in C1

Input x1, y1, r1, x2, y2, r2:
 5 4 2 5 4 3
C1  is in C2

Explanation:

Here is a breakdown of the above Python code:

• The code imports the "math" module.
• It prompts the user to input the coordinates and radii of two circles (x1, y1, r1, x2, y2, r2).
• It calculates the distance (d) between the centers of the two circles using the distance formula.
• The code checks the relationship between two circles based on their radii and distance.
• It prints the appropriate message indicating the relationship between the circles.

Flowchart:

For more Practice: Solve these Related Problems:

• Write a Python program to determine if one circle completely contains another given their centers and radii.
• Write a Python program to check if two circles are externally or internally tangent.
• Write a Python program to compute the distance between the boundaries of two circles given their centers and radii.
• Write a Python program to approximate the area of intersection between two overlapping circles.

Go to:

• Python Basic Exercises Home ↩
• Python Exercises Home ↩

Previous: Write a Python program to find the maximum sum of a contiguous subsequence from a given sequence of numbers a1, a2, a3, ... an. A subsequence of one element is also a continuous subsequence.
Next: Write a Python program to that reads a date (from 2016/1/1 to 2016/12/31) and prints the day of the date. Jan. 1, 2016, is Friday. Note that 2016 is a leap year.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.