Python: Find the first missing positive integer that does not exist in a given list

Last update on April 17 2025 13:01:14 (UTC/GMT +8 hours)

First Missing Positive Integer

Write a Python program to find the first missing positive integer that does not exist in a given list.

Sample Solution:

Python Code:

# Define a function to find the first missing positive integer in a list
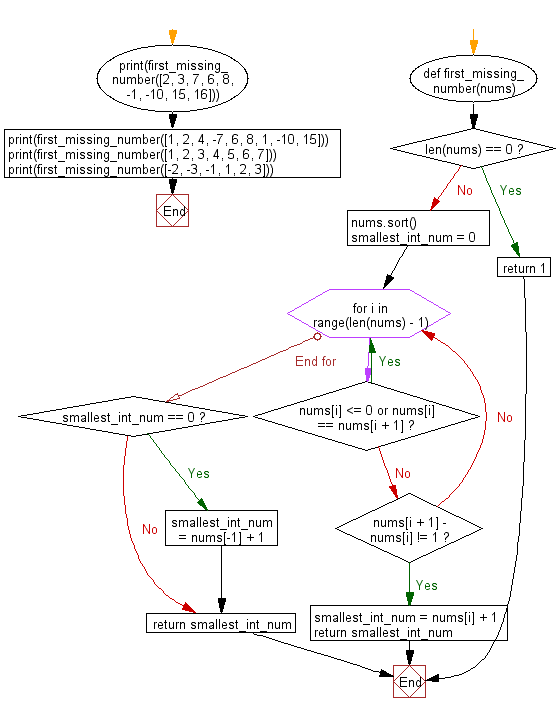
def first_missing_number(nums):
    # Check if the list is empty, return 1 if it is
    if len(nums) == 0:
        return 1
        
    # Sort the list in ascending order
    nums.sort()
    
    # Initialize the smallest positive integer as 0
    smallest_int_num = 0
    
    # Iterate through the sorted list
    for i in range(len(nums) - 1):
        # Skip non-positive or duplicate numbers
        if nums[i] <= 0 or nums[i] == nums[i + 1]:
            continue
        else:
            # Check for a gap between consecutive numbers
            if nums[i + 1] - nums[i] != 1:
                smallest_int_num = nums[i] + 1
                return smallest_int_num
    
    # If no gap is found, the smallest missing positive integer is after the last element
    if smallest_int_num == 0:
        smallest_int_num = nums[-1] + 1
    
    # Return the smallest missing positive integer
    return smallest_int_num

# Test the function with different lists of numbers
print(first_missing_number([2, 3, 7, 6, 8, -1, -10, 15, 16])) 
print(first_missing_number([1, 2, 4, -7, 6, 8, 1, -10, 15]))
print(first_missing_number([1, 2, 3, 4, 5, 6, 7]))
print(first_missing_number([-2, -3, -1, 1, 2, 3]))

Sample Output:

Explanation:

Here is a breakdown of the above Python code:

The function "first_missing_number()" takes a list of numbers ('nums') as input.
It checks if the list is empty and returns 1 if it is.
The function sorts the list in ascending order.
It initializes the smallest positive integer as 0.
It iterates through the sorted list, skipping non-positive or duplicate numbers.
It checks for a gap between consecutive numbers, indicating a missing positive integer.
If a gap is found, the smallest missing positive integer is determined and returned.
If no gap is found, the smallest missing positive integer is after the last element.
The function is tested with different lists of numbers.

Flowchart:

For more Practice: Solve these Related Problems:

Write a Python program to find the smallest missing positive integer in an unsorted array in O(n) time.
Write a Python program to identify the first missing positive number by rearranging the array elements in-place.
Write a Python program to determine the smallest positive integer that does not appear in a given list using index mapping.
Write a Python program to compute the first absent positive number using a constant space solution.

Go to:

Previous: Write a Python program to compute the largest product of three integers from a given list of integers.
Next: Write a Python program to randomly generate a list with 10 even numbers between 1 and 100 inclusive.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.