Python: Geometric progression

Last update on June 28 2025 12:43:30 (UTC/GMT +8 hours)

Generate Range with Ratio

Write a Python program to initialize a list containing the numbers in the specified range where start and end are inclusive and the ratio between two terms is step. Return an error if step equals 1.

Use range(), math.log() and math.floor() and a list comprehension to create a list of the appropriate length, applying the step for each element.
Omit the second argument, start, to use a default value of 1.
Omit the third argument, step, to use a default value of 2.

Sample Solution:

Python Code:

# Import the 'floor' and 'log' functions from the 'math' module.
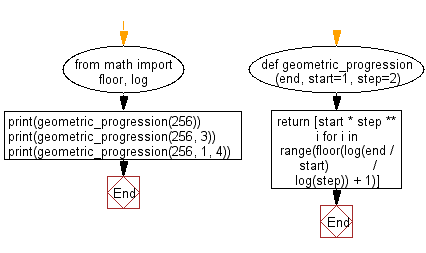
from math import floor, log

# Define a function 'geometric_progression' that calculates a geometric progression.
# It takes the ending value 'end' as a required parameter, and 'start' and 'step' as optional parameters with default values.
def geometric_progression(end, start=1, step=2):
    # Calculate the number of terms in the geometric progression using logarithms and floor division.
    num_terms = floor(log(end / start) / log(step) + 1)
    
    # Use a list comprehension to generate the geometric progression.
    progression = [start * step ** i for i in range(num_terms)]
    
    # Return the list representing the geometric progression.
    return progression

# Call the 'geometric_progression' function with different parameters and print the results.
print(geometric_progression(256))
print(geometric_progression(256, 3))
print(geometric_progression(256, 1, 4))

Sample Output:

[1, 2, 4, 8, 16, 32, 64, 128, 256]
[3, 6, 12, 24, 48, 96, 192]
[1, 4, 16, 64, 256]

Flowchart:

Flowchart: Geometric progression.

For more Practice: Solve these Related Problems:

Write a Python program to generate a geometric progression list given a start, end, and a ratio, and validate that the ratio is not 1.
Write a Python program to produce a list of numbers in a range where each term is the previous term multiplied by a specified ratio, with error handling for invalid ratios.
Write a Python program to create a list representing a geometric series from a starting number up to a maximum value using a given multiplier.
Write a Python program to generate a list of exponential values using a step ratio and then verify the integrity of the progression.

Go to:

Previous: Write a Python program to check if a given function returns True for every element in a list.
Next: Write a Python program to that takes any number of iterable objects or objects with a length property and returns the longest one.

Python Code Editor: