Python: Sieve of Eratosthenes method, for computing prime number

Last update on June 28 2025 12:47:57 (UTC/GMT +8 hours)

Compute Primes Using Sieve of Eratosthenes

Write a Python program that uses the Sieve of Eratosthenes method to compute prime numbers up to a specified number.

Note: In mathematics, the sieve of Eratosthenes (Ancient Greek: κόσκινον Ἐρατοσθένους, kóskinon Eratosthénous), one of a number of prime number sieves, is a simple, ancient algorithm for finding all prime numbers up to any given limit.

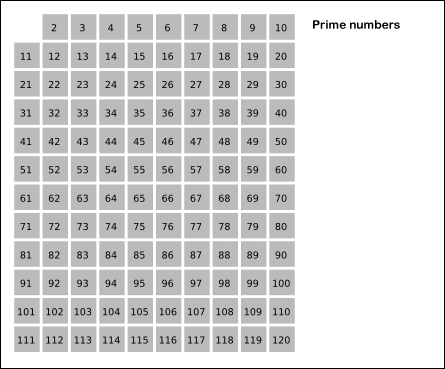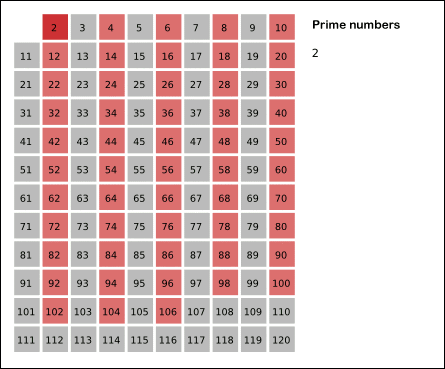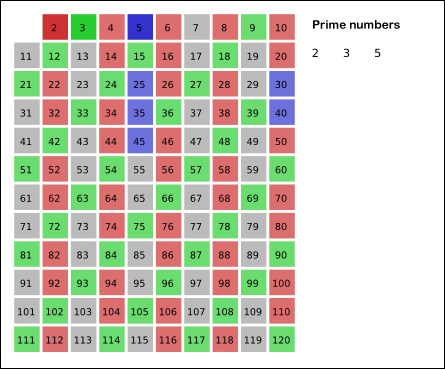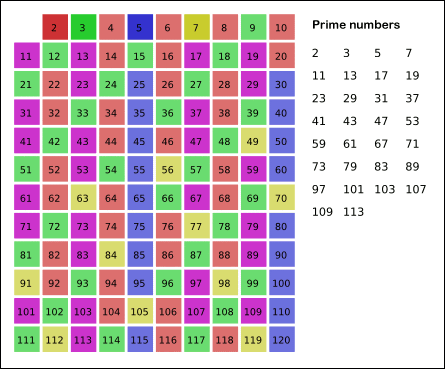
From Wikipedia Sieve of Eratosthenes: algorithm steps for primes below 121 (including optimization of starting from prime's square).

Sample Solution:

Python Code:

# Define a function named 'prime_eratosthenes' that generates prime numbers using the Sieve of Eratosthenes algorithm
def prime_eratosthenes(n):
    prime_list = []  # Create an empty list to store prime numbers
    # Iterate through the numbers from 2 to 'n'
    for i in range(2, n+1):
        if i not in prime_list:
            # If 'i' is not in the 'prime_list,' it's a prime number; print it
            print(i)

            # Mark all multiples of 'i' as non-prime by adding them to 'prime_list'
            for j in range(i*i, n+1, i):
                prime_list.append(j)

# Call the 'prime_eratosthenes' function with 'n' set to 100 to generate prime numbers
# The function does not have a return value, so it prints the prime numbers directly
prime_eratosthenes(100)

Sample Output:

2                                                                                                             
3                                                                                                             
5                                                                                                             
7                                                                                                             
11                                                                                                            
-------
79                                                                                                            
83                                                                                                            
89                                                                                                            
97                                                                                                            
None   

Flowchart:

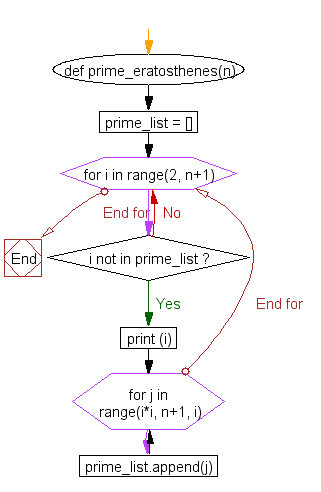
For more Practice: Solve these Related Problems:

• Write a Python program to find all prime numbers in a given range without using the Sieve of Eratosthenes.
• Write a Python program to generate prime numbers up to n using a segmented sieve.
• Write a Python program to compute the prime factors of a given number using the sieve method.
• Write a Python program to count the number of prime numbers in a given list using the sieve method.

Go to:

• Python Data Type List Exercises Home ↩
• Python Exercises Home ↩

Previous: Write a Python program to generate all sublists of a list.
Next: Write a Python program to create a list by concatenating a given list which range goes from 1 to n.

Python Code Editor: