Python Math: Computing square roots using the Babylonian method

Last update on April 24 2025 12:35:19 (UTC/GMT +8 hours)

18. Babylonian Square Root

Write a Python program to compute square roots using the Babylonian method.

Perhaps the first algorithm used for approximating √S is known as the Babylonian method, named after the Babylonians, or "Hero's method", named after the first-century Greek mathematician Hero of Alexandria who gave the first explicit description of the method. It can be derived from (but predates by 16 centuries) Newton's method. The basic idea is that if x is an overestimate to the square root of a non-negative real number S then S / x will be an underestimate and so the average of these two numbers may reasonably be expected to provide a better approximation.

Graph Presentation

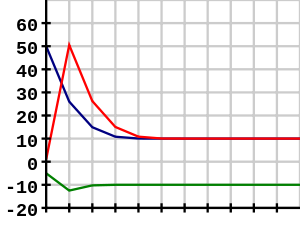
Graph charting the use of the Babylonian method for approximating the square root of 100 (10) using starting values x0 = 50, x0 = 1, and x0 = −5. Note that using a negative starting value yields the negative root.
Graph Credits: Crotalus Horridus

Sample Solution:

Python Code:

def BabylonianAlgorithm(number):
    if(number == 0):
        return 0;

    g = number/2.0;
    g2 = g + 1;
    while(g != g2):
        n = number/ g;
        g2 = g;
        g = (g + n)/2;

    return g;
print('The Square root of 0.3 =', BabylonianAlgorithm(0.3));

Sample Output:

The Square root of 0.3 = 0.5477225575051661

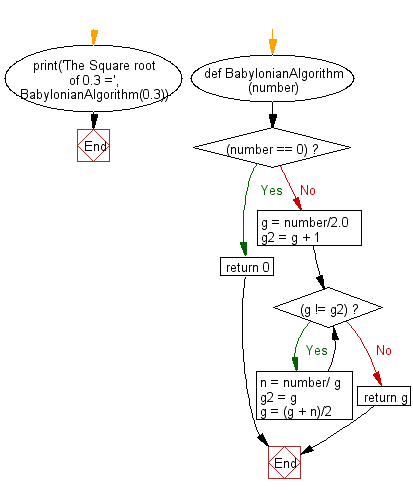
Flowchart:

$Flowchart: Computing square roots using Babylonian method$

For more Practice: Solve these Related Problems:

Write a Python program to compute the square root of a number using the Babylonian method and print each iteration until convergence.
Write a Python function that approximates the square root using the Babylonian method with a specified tolerance and returns the final value.
Write a Python script to compare the Babylonian method square root with math.sqrt() for a series of test values.
Write a Python program to implement the Babylonian algorithm to compute square roots and count the number of iterations required for convergence.

Go to:

Previous: Write a Python program to print the first n Lucky Numbers.
Next: Write a Python program to multiply two integers without using the * operator in python.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.