Python: Check whether a distinct pair of numbers whose product is odd present in a sequence of integer values

Python Basic: Exercise-150 with Solution

Odd Product Pair Checker

Write a Python function to check whether a distinct pair of numbers whose product is odd is present in a sequence of integer values.

Sample Solution:

Python Code :

# Define a function named 'odd_product' that takes a list 'nums' as its argument.
def odd_product(nums):
    # Iterate through the indices of the 'nums' list using nested loops.
    for i in range(len(nums)):
        for j in range(len(nums)):
            # Check if 'i' and 'j' are different indices to avoid multiplying the same number.
            if i != j:
                # Calculate the product of elements at indices 'i' and 'j'.
                product = nums[i] * nums[j]
                # Check if the product is an odd number (using bitwise AND with 1).
                if product & 1:
                    # If an odd product is found, return True immediately.
                    return True
    # If no odd product is found, return False.
    return False

# Define three lists of integers.
dt1 = [2, 4, 6, 8]
dt2 = [1, 6, 4, 7, 8]
dt3 = [1, 3, 5, 7, 9]

# Call the 'odd_product' function for each list and print the result.
print(dt1, odd_product(dt1))
print(dt2, odd_product(dt2))
print(dt3, odd_product(dt3))

Sample Output:

[2, 4, 6, 8] False
[1, 6, 4, 7, 8] True
[1, 3, 5, 7, 9] True

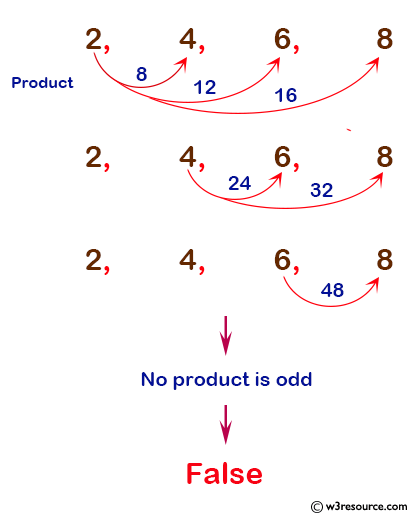
Pictorial Presentation of the sequence [2, 4, 6, 8]:

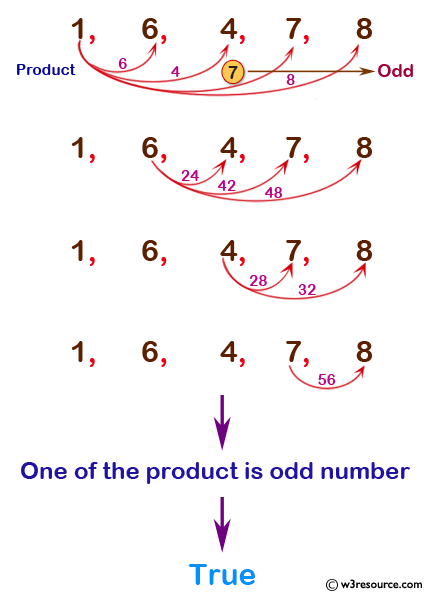
Pictorial Presentation of the sequence [1, 6, 4, 7, 8]:

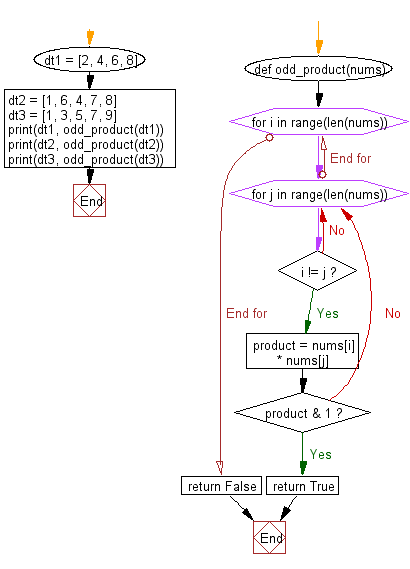
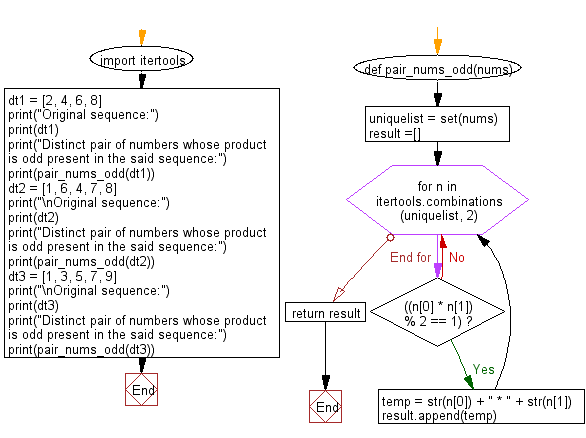
Flowchart:

Sample Solution:

Distinct pair of numbers whose product is odd present in a given sequence:

Python Code :

# Import the itertools module to work with combinations of numbers.
import itertools

# Define a function named 'pair_nums_odd' that takes a list 'nums' as its argument.
def pair_nums_odd(nums):
    # Create a set of unique numbers from the input list.
    uniquelist = set(nums)
    # Initialize an empty list 'result' to store pairs whose product is odd.
    result = []
    # Iterate through all distinct pairs of numbers from 'uniquelist'.
    for n in itertools.combinations(uniquelist, 2):
        # Check if the product of the pair is an odd number.
        if ((n[0] * n[1]) % 2 == 1):
            # Create a string representation of the pair.
            temp = str(n[0]) + " * " + str(n[1])
            # Append the string to the 'result' list.
            result.append(temp)
    # Return the list of distinct pairs with odd products.
    return result

# Define three lists of integers.
dt1 = [2, 4, 6, 8]
dt2 = [1, 6, 4, 7, 8]
dt3 = [1, 3, 5, 7, 9]

# Print the original sequence and the distinct pairs with odd products for each list.
print("Original sequence:")
print(dt1)
print("Distinct pair of numbers whose product is odd present in the said sequence:")
print(pair_nums_odd(dt1))

print("\nOriginal sequence:")
print(dt2)
print("Distinct pair of numbers whose product is odd present in the said sequence:")
print(pair_nums_odd(dt2))

print("\nOriginal sequence:")
print(dt3)
print("Distinct pair of numbers whose product is odd present in the said sequence:")
print(pair_nums_odd(dt3))

Sample Output:

Original sequence:
[2, 4, 6, 8]
Distinct pair of numbers whose product is odd present in the said sequence:
[]

Original sequence:
[1, 6, 4, 7, 8]
Distinct pair of numbers whose product is odd present in the said sequence:
['1 * 7']

Original sequence:
[1, 3, 5, 7, 9]
Distinct pair of numbers whose product is odd present in the said sequence:
['1 * 3', '1 * 5', '1 * 7', '1 * 9', '3 * 5', '3 * 7', '3 * 9', '5 * 7', '5 * 9', '7 * 9']

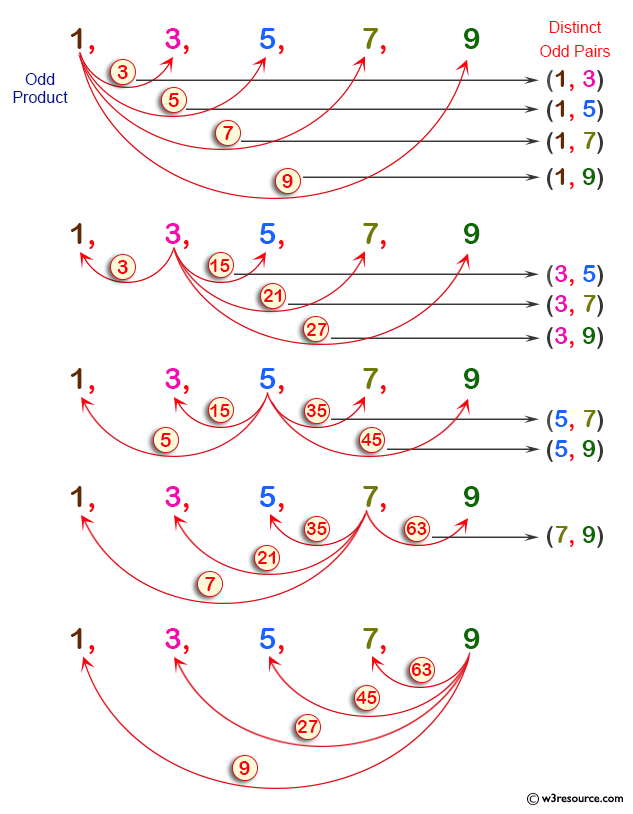
Pictorial Presentation of the sequence [1, 3, 5, 7, 9]:

Flowchart:

Python Code Editor :

Previous: Write a Python function that takes a positive integer and returns the sum of the cube of all the positive integers smaller than the specified number.
Next: Basic - Part-II.