Python: Function that takes a positive integer and returns the sum of the cube of all the positive integers smaller than the specified number

Python Basic: Exercise-149 with Solution

Cube Sum of Smaller Integers

Write a Python function that takes a positive integer and returns the sum of the cube of all positive integers smaller than the specified number.

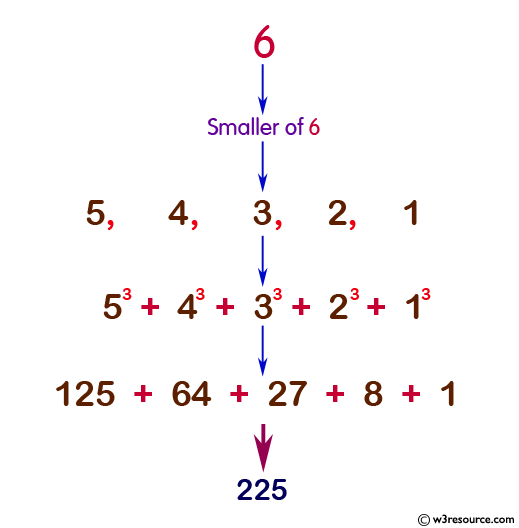
Ex.: 8 = 7³+6³+5³+4³+3³+2³+1³ = 784

Sample Solution-1:

Python Code:

# Define a function named 'sum_of_cubes' that takes an integer 'n' as its argument.
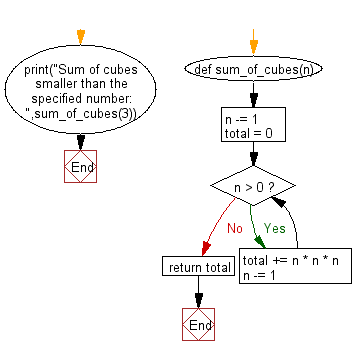
def sum_of_cubes(n):
    # Decrement 'n' by 1 to exclude 'n' itself from the sum.
    n -= 1
    # Initialize a variable 'total' to keep track of the sum of cubes.
    total = 0
    
    # Use a 'while' loop to iterate through numbers from 'n-1' down to 1.
    while n > 0:
        # Calculate the cube of the current number 'n' and add it to 'total'.
        total += n * n * n
        # Decrement 'n' by 1 for the next iteration.
        n -= 1
    
    # Return the total sum of cubes.
    return total

# Call the 'sum_of_cubes' function with an argument '3' and print the result.
print("Sum of cubes smaller than the specified number: ", sum_of_cubes(3))

Sample Output:

Sum of cubes smaller than the specified number:  9

Pictorial Presentation:

Flowchart:

Sample Solution-2:

Python Code:

# Define a function named 'sum_of_cubes' that takes an integer 'n' as its argument.
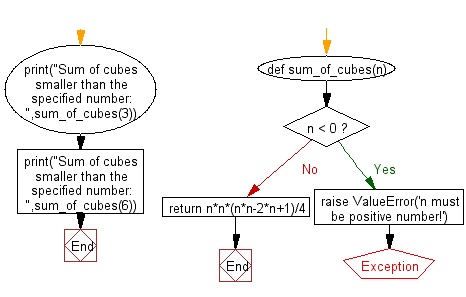
def sum_of_cubes(n):
    # Check if 'n' is less than 0, and if so, raise a ValueError with a specific message.
    if n < 0:
        raise ValueError('n must be a positive number!')
    
    # Calculate the sum of cubes using the formula (n^2 * (n^2 - 2n + 1)) / 4.
    # This formula is derived from the sum of the first 'n' cubes.
    return n * n * (n * n - 2 * n + 1) / 4

# Call the 'sum_of_cubes' function with an argument '3' and print the result.
print("Sum of cubes smaller than the specified number (n=3): ", sum_of_cubes(3))

# Call the 'sum_of_cubes' function with an argument '6' and print the result.
print("Sum of cubes smaller than the specified number (n=6): ", sum_of_cubes(6))

Sample Output:

Sum of cubes smaller than the specified number:  9.0
Sum of cubes smaller than the specified number:  225.0

Flowchart:

Sample Solution-3:

Python Code:

# Define a function named 'sum_of_cubes' that takes an integer 'n' as its argument.
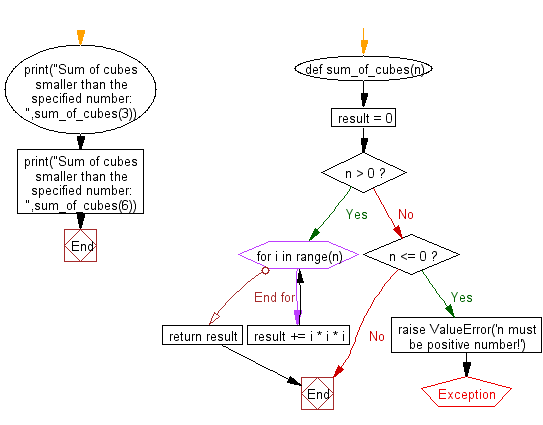
def sum_of_cubes(n):
    # Initialize a variable 'result' to store the sum of cubes.
    result = 0
    
    # Check if 'n' is greater than 0.
    if n > 0:
        # Iterate through numbers from 0 to 'n-1' and add the cube of each number to 'result'.
        for i in range(n):
            result += i * i * i
        
        # Return the calculated 'result'.
        return result
    # If 'n' is not greater than 0, raise a ValueError with a specific message.
    elif n <= 0:
        raise ValueError('n must be a positive number!')

# Call the 'sum_of_cubes' function with an argument '3' and print the result.
print("Sum of cubes smaller than the specified number (n=3): ", sum_of_cubes(3))

# Call the 'sum_of_cubes' function with an argument '6' and print the result.
print("Sum of cubes smaller than the specified number (n=6): ", sum_of_cubes(6))

Sample Output:

Sum of cubes smaller than the specified number:  9
Sum of cubes smaller than the specified number:  225

Flowchart:

Python Code Editor :

Previous: Write a Python function to find the maximum and minimum numbers from a sequence of numbers.
Next: Write a Python function to check whether a distinct pair of numbers whose product is odd present in a sequence of integer values.