C Exercises: Calculate e raise to the power x using sum of first n terms of Taylor Series

Last update on August 07 2025 12:49:49 (UTC/GMT +8 hours)

24. Exponential Taylor Series Variants

Write a C program to calculate e raised to the power of x using the sum of the first n terms of the Taylor Series.

From Wikipedia,
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point.
Example:
The Taylor series for any polynomial is the polynomial itself.

The above expansion holds because the derivative of e^x with respect to x is also e^x, and e⁰ equals 1.
This leaves the terms (x − 0)ⁿ in the numerator and n! in the denominator for each term in the infinite sum.

Example:
Input: n = 25
float x = 5.0
Output: e^x = 148.413162

Sample Solution:

C Code:

#include <stdio.h>
#include <stdlib.h>

// Function to calculate the exponential function using Taylor series approximation
float Taylor_exponential(int n, float x) { 
    float exp_sum = 1; // Initialize the sum as 1 (initial term of Taylor series)

    // Loop to calculate each term of the Taylor series for the exponential function
    for (int i = n - 1; i > 0; --i) {
        exp_sum = 1 + x * exp_sum / i; // Calculate the next term of the series and update the sum
    }

    return exp_sum; // Return the final result of the Taylor series approximation for e^x
}

// Main function
int main(void) {
    int n = 25; // Number of terms for Taylor series
    float x = 5.0; // Value of x in e^x

    // Check if n and x are greater than 0 before proceeding
    if (n > 0 && x > 0) {
        printf("value of n = %d and x = %f ", n, x);
        printf("\ne^x = %f", Taylor_exponential(n, x)); // Calculate and print the result of e^x
    }

    return 0;
}

Sample Output:

value of n = 25 and x = 1968710504 
e^x = 148.413162

Flowchart:

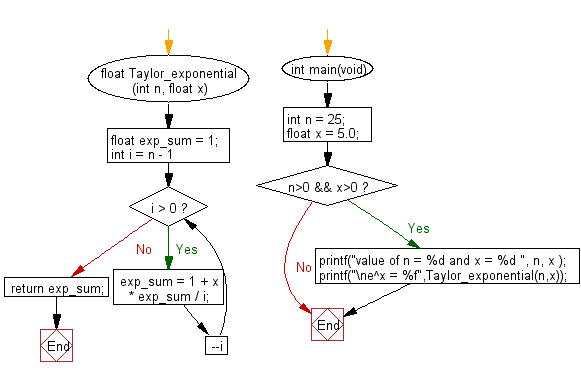
For more Practice: Solve these Related Problems:

• Write a C program to compute e^x using the Taylor series expansion with a specified number of terms.
• Write a C program to approximate e^x and compare the result with the math library function for accuracy.
• Write a C program to calculate e^x using an iterative summation of series terms until convergence.
• Write a C program to implement the Taylor series for e^x using recursion to compute each term.

Go to:

• C Programming Math Exercises Home ↩
• C Programming Exercises Home ↩

PREV : Next Smallest Palindrome Variants.
NEXT : Prime Factorization Variants.

C Programming Code Editor:

Click to Open Editor

Improve this sample solution and post your code through Disqus.