Java: Accept a even number from the user and create a combinations that express the given number as a sum of two prime numbers

Java Basic: Exercise-233 with Solution

Goldbach Combinations of Even Number

Write a Java program that accepts an even number (n should be greater than or equal to 4 and less than or equal to 50,000, a Goldbach number) from the user and creates combinations that express the given number as a sum of two prime numbers. Print the number of combinations.

Goldbach number: A Goldbach number is a positive even integer that can be expressed as the sum of two odd primes.[4] Since four is the only even number greater than two that requires the even prime 2 in order to be written as the sum of two primes, another form of the statement of Goldbach's conjecture is that all even integers greater than 4 are Goldbach numbers.
The expression of a given even number as a sum of two primes is called a Goldbach partition of that number. The following are examples of Goldbach partitions for some even numbers:
6 = 3 + 3
8 = 3 + 5
10 = 3 + 7 = 5 + 5
12 = 7 + 5
...
100 = 3 + 97 = 11 + 89 = 17 + 83 = 29 + 71 = 41 + 59 = 47 + 53

Visual Presentation:

Sample Solution:

Java Code:

// Importing necessary classes for input/output operations
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

// Main class named "Main"
public class Main {

    // Main method to execute the program, throws NumberFormatException and IOException
    public static void main(String[] args) throws NumberFormatException, IOException {

        // Creating BufferedReader and StringBuilder objects for efficient input and output
        BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder builder = new StringBuilder();

        // Setting the maximum value for calculations
        int max = 50000;

        // Prompting the user to input an even number
        System.out.print("Input an even number: ");

        // Creating a boolean array to store information about prime numbers
        boolean[] primes = new boolean[max + 1];

        // Initializing count variable to count prime numbers
        int count = 1;

        // Looping through odd numbers to find prime numbers using the Sieve of Eratosthenes algorithm
        for (int i = 3; i <= max; i += 2) {
            if (!primes[i]) {
                count++;
                // Marking multiples of the current prime number as non-prime
                if (i <= Math.sqrt(max)) {
                    for (int j = i; j <= max / i; j += 2) {
                        primes[(int) (i * j)] = true;
                    }
                }
            }
        }

        // Creating an array to store prime numbers
        int[] prime = new int[count];
        prime[0] = 2;
        int count2 = 1;

        // Filling the prime array with prime numbers
        for (int i = 3; i <= max; i += 2) {
            if (!primes[i]) {
                prime[count2] = i;
                count2++;
            }
        }

        // Creating an array to store the count of combinations for each sum of two prime numbers
        int[] g = new int[max + 1];

        // Calculating the count of combinations for each sum of two prime numbers
        for (int i = 0; i <= prime.length; i++) {
            for (int j = i; j < prime.length && prime[i] + prime[j] <= max; j++) {
                g[prime[i] + prime[j]]++;
            }
        }

        // Reading the input value for which we want to find the count of combinations
        int n = Integer.parseInt(reader.readLine());

        // Appending the count of combinations to the StringBuilder
        builder.append(g[n]).append('\n');

        // Outputting the number of combinations
        System.out.print("\nNumber of combinations: ");
        System.out.print(builder);
    }
} 

Sample Output:

Input an even number: 100

Number of combinations: 6

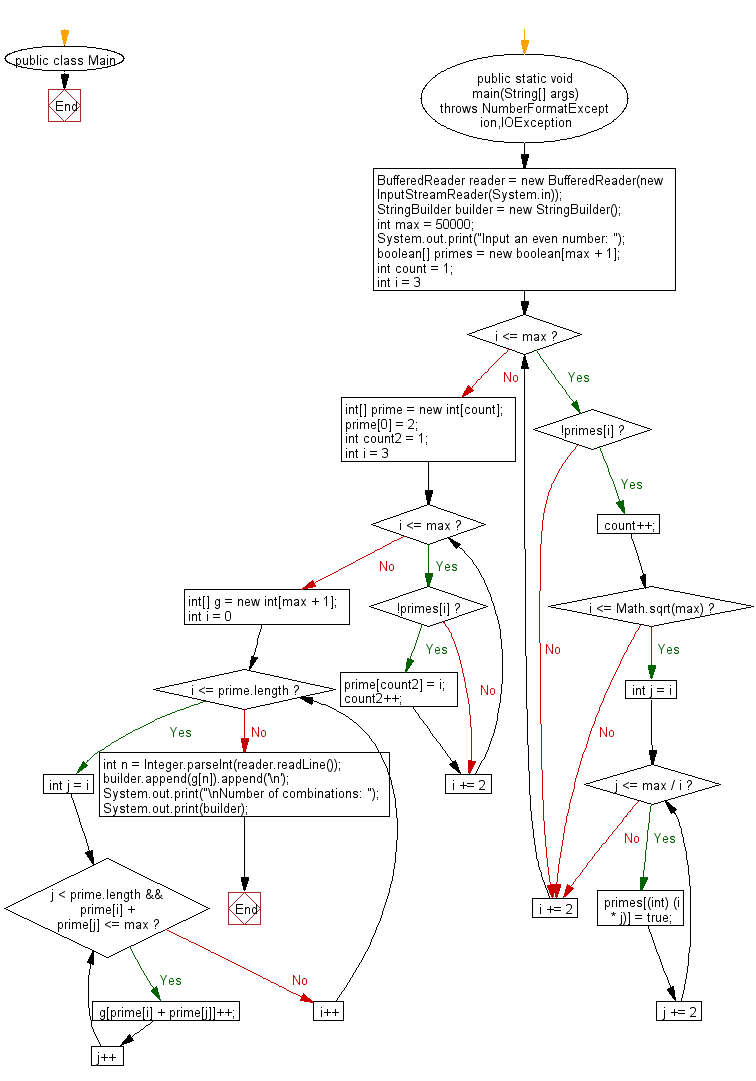
Flowchart:

Java Code Editor:

Contribute your code and comments through Disqus.

Previous: Write a Java program to compute the sum of first n given prime numbers.
Next: Write a Java program to create maximum number of regions obtained by drawing n given straight lines.