JavaScript: Find a perfect number

JavaScript Function: Exercise-12 with Solution

Check Perfect Number

Write a JavaScript function that checks whether a number is perfect.

Note : According to Wikipedia : In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself (also known as its aliquot sum). Equivalently, a perfect number is a number that is half the sum of all of its positive divisors (including itself).
Example : The first perfect number is 6, because 1, 2, and 3 are its proper positive divisors, and 1 + 2 + 3 = 6. Equivalently, the number 6 is equal to half the sum of all its positive divisors: ( 1 + 2 + 3 + 6 ) / 2 = 6. The next perfect number is 28 = 1 + 2 + 4 + 7 + 14. This is followed by the perfect numbers 496 and 8128.

Visual Presentation:

Sample Solution-1:

JavaScript Code:

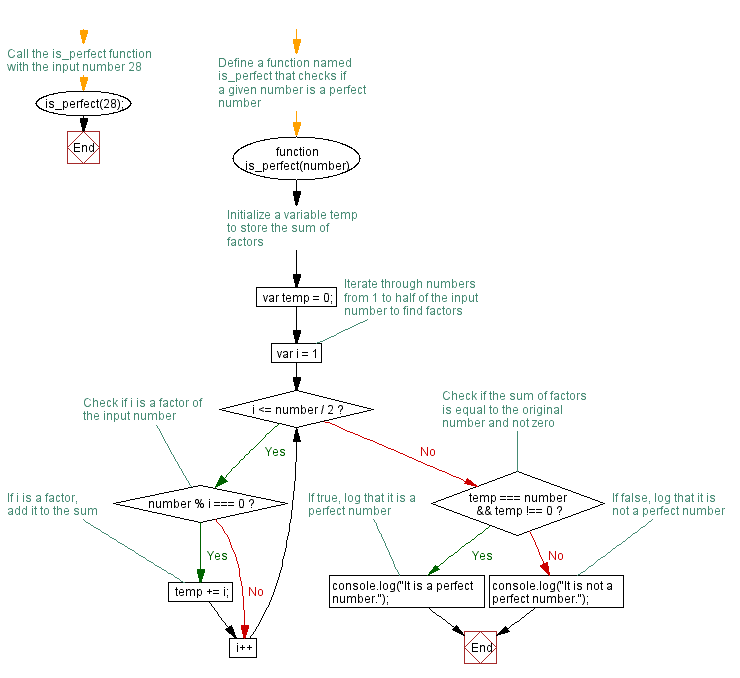
// Define a function named is_perfect that checks if a given number is a perfect number
function is_perfect(number) {
  // Initialize a variable temp to store the sum of factors
  var temp = 0;

  // Iterate through numbers from 1 to half of the input number to find factors
  for (var i = 1; i <= number / 2; i++) {
    // Check if i is a factor of the input number
    if (number % i === 0) {
      // If i is a factor, add it to the sum
      temp += i;
    }
  }

  // Check if the sum of factors is equal to the original number and not zero
  if (temp === number && temp !== 0) {
    // If true, log that it is a perfect number
    console.log("It is a perfect number.");
  } else {
    // If false, log that it is not a perfect number
    console.log("It is not a perfect number.");
  }
}

// Call the is_perfect function with the input number 28
is_perfect(28); 

Output:

It is a perfect number.

Flowchart:

Live Demo:

See the Pen JavaScript - Find a perfect number-function-ex- 12 by w3resource (@w3resource) on CodePen.

Sample Solution-2:

JavaScript Code:

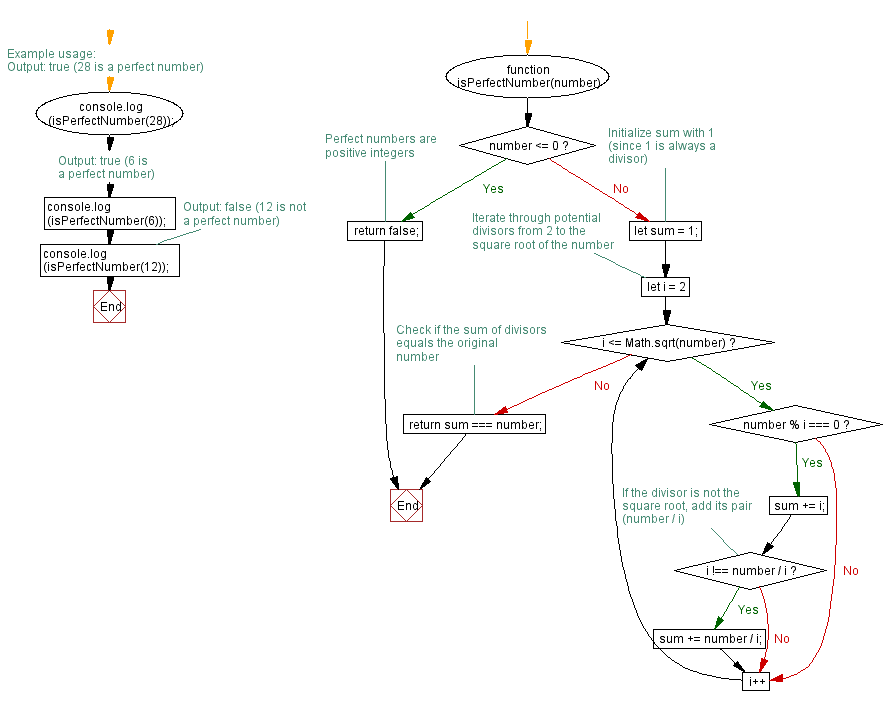
function isPerfectNumber(number) {
    if (number <= 0) {
        return false; // Perfect numbers are positive integers
    }

    let sum = 1; // Initialize sum with 1 (since 1 is always a divisor)

    // Iterate through potential divisors from 2 to the square root of the number
    for (let i = 2; i <= Math.sqrt(number); i++) {
        if (number % i === 0) {
            sum += i;
            // If the divisor is not the square root, add its pair (number / i)
            if (i !== number / i) {
                sum += number / i;
            }
        }
    }

    // Check if the sum of divisors equals the original number
    return sum === number;
}

// Example usage:
console.log(isPerfectNumber(28)); // Output: true (28 is a perfect number)
console.log(isPerfectNumber(6));  // Output: true (6 is a perfect number)
console.log(isPerfectNumber(12)); // Output: false (12 is not a perfect number)

Output:

true
true
false

Flowchart:

For more Practice: Solve these Related Problems:

• Write a JavaScript function that checks if a number is perfect by recursively summing its proper divisors.
• Write a JavaScript function that determines whether a number is perfect and returns both a boolean flag and its divisor sum.
• Write a JavaScript function that checks for a perfect number using array methods instead of explicit loops.
• Write a JavaScript function that verifies if a number is perfect and properly handles edge cases such as negative numbers and zero.

Improve this sample solution and post your code through Disqus.

Previous: Write a JavaScript function which will take an array of numbers stored and find the second lowest and second greatest numbers, respectively.
Next: Write a JavaScript function to compute the factors of a positive integer.