Python: Count number of zeros and ones in the binary representation of a given integer

Python Basic - 1: Exercise-131 with Solution

Write a Python program to count the number of zeros and ones in the binary representation of a given integer.

Sample Solution

Python Code:

def test(num):
    ones =  bin(num). replace("0b", "").count('1')
    zeros = bin(num). replace("0b", "").count('0')
    return "Number of zeros: " + str(zeros) + ", Number of ones: " + str(ones);

n = 12; 
print("Original number: ",n);
print("Number of ones and zeros in the binary representation of the said number:");
print(test(n));
n = 1234;
print("\nOriginal number: ",n);
print("Number of ones and zeros in the binary representation of the said number:");
print(test(n));

Sample Output:

Original number:  12
Number of ones and zeros in the binary representation of the said number:
Number of zeros: 2, Number of ones: 2

Original number:  1234
Number of ones and zeros in the binary representation of the said number:
Number of zeros: 6, Number of ones: 5

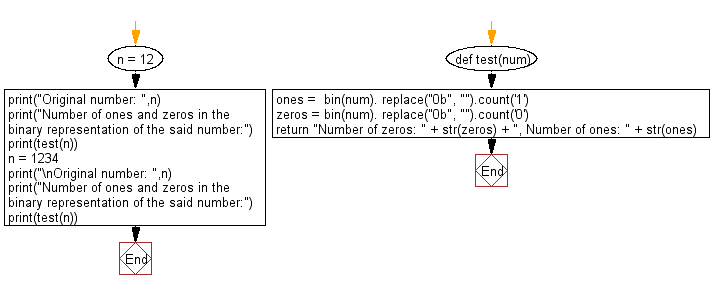
Flowchart:

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.

Previous: Write a Python program to check whether a given month and year contains a Monday 13^th.
Next: Write a Python program to find all the factors of a given natural number.