Python: Accept a positive number and subtract from this number the sum of its digits

Last update on May 24 2025 10:49:17 (UTC/GMT +8 hours)

Subtract Sum of Digits

Write a Python program that accepts a positive number and subtracts from it the sum of its digits, and so on. Continue this operation until the number is positive.

Sample Solution:

Python Code:

# Define a function 'repeat_times' that repeatedly subtracts the sum of the digits
# of a number from the number until it becomes non-positive, and then returns the result.
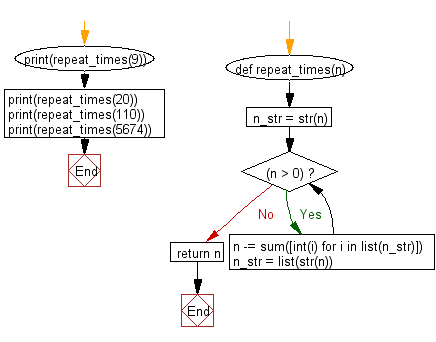
def repeat_times(n):
    # Convert the input number 'n' to a string for digit manipulation.
    n_str = str(n)
    
    # Continue the loop while 'n' is greater than 0.
    while n > 0:
        # Subtract the sum of the digits of 'n' from 'n'.
        n -= sum([int(i) for i in list(n_str)])
        
        # Update 'n_str' with the string representation of the updated 'n'.
        n_str = list(str(n))
    
    # Return the final value of 'n'.
    return n

# Test the 'repeat_times' function with different values of 'n' and print the results.
print(repeat_times(9))
print(repeat_times(20))
print(repeat_times(110))
print(repeat_times(5674))

Sample Output:

0
0
0
0

Explanation:

The above Python code defines a function named "repeat_times()" that repeatedly subtracts the sum of the digits of a number from the number until the number becomes non-positive. Here's a brief explanation:

• Function Definition:
• def repeat_times(n):: Define a function named "repeat_times()" that takes an integer n as input.
• Convert to String:
• n_str = str(n): Convert the input number 'n' to a string for digit manipulation.
• Repetition Loop:
• while n > 0:: Continue the loop while 'n' is greater than 0.
• n -= sum([int(i) for i in list(n_str)]): Subtract the sum of the digits of 'n' from 'n'.
• n_str = list(str(n)): Update 'n_str' with the string representation of the updated 'n'.
• Return Result:
• return n: Return the final value of 'n' after it becomes non-positive.
• Function Testing:
• Test the "repeat_times()" function with different values of 'n' (9, 20, 110, 5674).
• Print the results of the function calls.

Flowchart:

For more Practice: Solve these Related Problems:

• Write a Python program to repeatedly subtract the product of a number’s digits from the number until a single digit is obtained.
• Write a Python program that alternates between subtracting the sum and the product of the digits from a number until convergence.
• Write a Python program to subtract only the sum of even digits from a number repeatedly until a fixed point is reached.
• Write a Python program to repeatedly subtract the digital root of a number until it stabilizes.

Previous: Write a Python program to create a sequence where the first four members of the sequence are equal to one, and each successive term of the sequence is equal to the sum of the four previous ones. Find the Nth member of the sequence.
Next: Write a Python program to find the number of divisors of a given integer is even or odd.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.