Python: Print the number of prime numbers which are less than or equal to a given integer

Last update on April 17 2025 13:05:50 (UTC/GMT +8 hours)

Count Prime Numbers

Write a Python program to print the number of prime numbers that are less than or equal to a given number.

Input:
n (1 ≤ n ≤ 999,999)
Input the number(n): 35
Number of prime numbers which are less than or equal to n.: 11

Sample Solution:

Python Code:

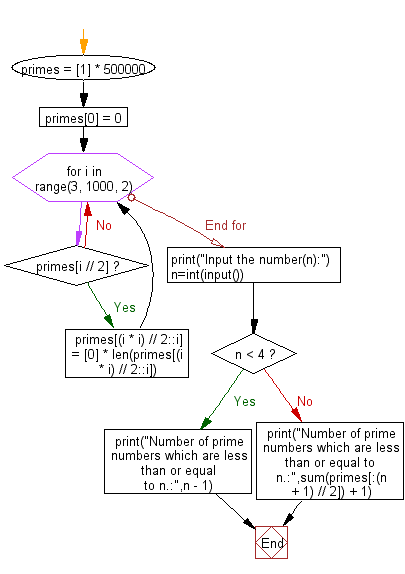
# Initialize a list to represent prime numbers up to 500000
primes = [1] * 500000
primes[0] = 0  # 0 is not a prime number

# Sieve of Eratosthenes: Mark non-prime numbers in the list
for i in range(3, 1000, 2):
    if primes[i // 2]:
        primes[(i * i) // 2::i] = [0] * len(primes[(i * i) // 2::i])

# Prompt user to input a number 'n'
print("Input the number(n):")
n = int(input())

# Check and print the number of primes less than or equal to 'n'
if n < 4:
    print("Number of prime numbers which are less than or equal to n.:", n - 1)
else:
    print("Number of prime numbers which are less than or equal to n.:", sum(primes[:(n + 1) // 2]) + 1)

Sample Output:

Input the number(n):
 35
Number of prime numbers which are less than or equal to n.: 11

Explanation:

Here is a breakdown of the above Python code:

• Initialize Prime List:
• primes is initialized as a list of 1s, where the index represents numbers. primes[0] is set to 0 since 0 is not a prime number.
• Sieve of Eratosthenes:
• The code uses the Sieve of Eratosthenes algorithm to mark non-prime numbers in the list. It iterates over odd numbers from 3 to 999 (skipping even numbers) and updates the list to mark multiples of each prime.
• User Input:
• The user is prompted to input a number 'n'.
• Check and Print Prime Count:
• If 'n' is less than 4, it prints n - 1 as the count of prime numbers (excluding 0). Otherwise, it prints the count of prime numbers less than or equal to 'n' using the precomputed 'primes' list.

Visual Presentation:




Flowchart:





For more Practice: Solve these Related Problems:

• Write a Python program to compute the sum of all prime numbers less than or equal to a given number.
• Write a Python program to generate and display a list of all prime numbers up to a specified limit.
• Write a Python program to count the number of twin prime pairs below a given number.
• Write a Python program to find the largest gap between consecutive prime numbers within a given range.



Go to:

• Python Basic Exercises Home ↩
• Python Exercises Home ↩



Previous: Write a Python program which reads an integer n and find the number of combinations of a,b,c and d (0 ≤ a,b,c,d ≤ 9) where (a + b + c + d) will be equal to n.
Next: Write a program to compute the radius and the central coordinate (x, y) of a circle which is constructed by three given points on the plane surface.

Python Code Editor:

Have another way to solve this solution? Contribute your code (and comments) through Disqus.